
|
|
 |
|
|
|
|
 |
Temas de Estadística
Práctica Antonio Roldán Martínez |
|
|
Distribuciones bidimensionales |
||
|
Estás en Inicio > Estadística > Tema 5 - Distribuciones bidimensionales. Regresión. |
||
Cuestión-ejemplo
Prácticas
Ejercicios
Uso en el aula
Para ampliar
Regresión no lineal
Relaciones alométricas
Resumen teórico
| Cuestión - Ejemplo |
¿Tendré que estudiar mucho para sacar notable? |
Un grupo de Enseñanza Secundaria ha elaborado una encuesta sobre las horas diarias que emplean en el estudio y la calificación obtenida en Matemáticas en el último examen.
Han recogido los resultados en la siguiente tabla:
| Horas de estudio | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 4 | 4 | 5 |
| Calificación | 2 | 1 | 3 | 4 | 3 | 2 | 2 | 4 | 5 | 7 | 8 | 6 | 5 | 8 | 10 | 7 |
Además de estudiar el grado de asociación entre las dos variables, que ya se explicó en el tema anterior mediante el coeficiente de correlación, nos puede interesar hacer pronósticos: ¿Qué nota puedo esperar si estudio 2 horas y meda? Para realizar esos pronósticos usaremos las técnicas de Regresión.
Puede ser interesante, en primer lugar, determinar el grado de paralelismo que existe entre ambas variables.
Abre el archivo regresion.ods, que te servirá para desarrollar la práctica.
Descarga y estudia el documento practica51.pdf
Si no lo has realizado ya, descarga el documento de teoría
Una vez realizada la práctica, abre el documento minimocuad.pdf para profundizar en el tema.
Construcción de un modelo para el estudio de la Regresión
En esta práctica partirás de una hoja de cálculo en blanco, y deberás construir sobre ella un modelo.
Si tienes dificultades en algún detalle de la confección de este modelo, puedes consultar bidim0.ods en la carpeta de modelos de esta sesión.
Desarrolla la práctica siguiendo el contenido del documento practica52.pdf
Abre el archivo regconfrec.ods. Contiene un modelo de regresión ya confeccionado.
Con él desarrollarás la práctica 3, siguiendo el documento practica53.pdf
La población del pueblo de Andrés ha seguido esta evolución en los últimos quinquenios (redondeando a cientos)
| Año | Población |
| 1970 | 8200 |
| 1975 | 8700 |
| 1980 | 8900 |
| 1985 | 9900 |
| 1990 | 10000 |
| 1995 | 10500 |
| 2000 | 11200 |
Copia estos datos en el modelo que has creado en la Práctica 2 y lee los resultados para ver si coinciden con estos

¿Qué población esperaríamos para 2005 y 2010?
Usa las celdas que has creado para pronósticos que están fuera de la tabla. Te debe dar:
Y´(2005) = 11585 habitantes
Y´(2010) = 12.075 hab.
El error típico es 184, que es la desviación típica de los errores. Repasa su columna y observarás que todos son de esa magnitud. Como verás en otro tema, es raro que un error supere el doble del error típico, es decir 184*2 = 368 habitantes. De hecho, se cumple en este ejemplo.
En un viaje muy aburrido, Elena anota la hora cada vez que pasa el coche familiar por puntos kilométricos múltiplos de 20. El resultado de su entretenimiento es el siguiente:
| Minutos | Kilómetros |
| 0 | 0 |
| 10 | 20 |
| 28 | 40 |
| 41 | 60 |
| 55 | 80 |
| 70 | 100 |
| 86 | 120 |
| 98 | 140 |
Pronostica: A) En qué minuto pasó por el km. 75 B) Dónde se encontraban al cumplir la primera hora.
Usa tu modelo.
A) En el minuto 52 B) En el kilómetro 86
Ejercicio 3
Una empresa de electrónica ha lanzado un producto nuevo, que como todos los de su clase, presenta la llamada "enfermedad infantil", ya que en los primeros envíos suelen abundar los pequeños problemas hasta que la producción se estabiliza. Para estudiar las incidencias, se ha recogido en una tabla el número de llamadas realizadas al servicio técnico de una zona elegida al azar por averías en el nuevo producto, durante 6 meses. Los datos se recogen en la tabla siguiente:
| Seis primeros meses | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Llamadas por día | 0 | 0 | 1 | 3 | 5 | 6 | 9 |
| 1 | 0 | 5 | 3 | 5 | 12 | 9 | |
| 2 | 2 | 3 | 6 | 7 | 2 | 0 | |
| 3 | 1 | 8 | 6 | 3 | 0 | 4 | |
| 4 | 7 | 4 | 3 | 2 | 2 | 1 | |
| 5 | 6 | 4 | 0 | 1 | 0 | 1 | |
| 6 | 6 | 2 | 3 | 1 | 1 | 1 | |
| 7 | 1 | 0 | 1 | 0 | 0 | 0 | |
| 8 | 1 | 0 | 0 | 1 | 0 | 0 | |
La variable X corresponde a los seis meses de recogida de datos, y la Y el número de llamadas habidas en un día. Las frecuencias interiores representan el número de días en los que se han recibido las llamadas representadas por la variable Y.
Traslada esta tabla (sólo la parte de color amarillo) a la hoja de cálculo regconfrec.ods. de esta sesión. Resuelve, con esa herramienta, las siguientes cuestiones:
(a) La gráfica conjunta resultante presenta una tendencia hacia un máximo al fondo de la misma.
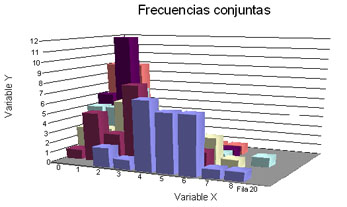
¿En qué meses y para qué número de llamadas se presenta la zona de máximos? ¿Qué significado tiene esto para el seguimiento de las averías?
(b) A la vista de la distribución de medias condicionadas de Y, que evidentemente posee una tendencia decreciente (observa la gráfica marginal de Y), ¿podemos afirmar que el número de llamadas se va concentrando alrededor de la media con el transcurso de los meses?. Pasa a la hoja Cálculos y estudia qué datos de la tabla nos darían esa información.
(c) Usa la hoja Pronósticos para averiguar en qué mes las averías dejarían de ser un problema importante.
Modelo similar al que se propone construir en la práctica 2, pero conteniendo pronósticos y gráficos. Es muy útil para ejercicios de interpretación de las tablas en los que el objetivo no son los cálculos. En su segunda hoja permite pronósticos puntuales, para interpolar y extrapolar con gran rapidez.
Esta hoja está diseñada para comprobar que la suma de errores cuadráticos respecto a una recta se minimiza si esta es la de regresión. Tienes una pequeña experiencia en el documento minimocuad.pdf
Permite realizar los cálculos de regresión en el caso en el que cada par de datos XY viene acompañado de la frecuencia correspondiente.
Realiza los cálculos de regresión en el caso de frecuencias conjuntas en una tabla de doble entrada.
Esta hoja de cálculo agrupa todos los casos de regresión lineal y no lineal. La consulta del valor del coeficiente de determinación R2 permite elegir la tendencia que minimiza los errores cuadráticos y conseguir así la función que mejor representa los datos.
exponencial.ods, potencial.ods, logaritmica.ods y cuadratica.ods
Son cuatro hojas que recogen las mismas técnicas que tendencias.ods, pero de forma separada.
son archivos auxiliares del documento bidim.pdf
Es un documento preparado para guiar a los alumnos en el aprendizaje de los conceptos y las técnicas referentes a las distribuciones bidimensionales en las que las variables son cuantitativas. Permite un repaso de conceptos o bien, con la ayuda de los profesores, para iniciar el tema.
Cuando unos datos no siguen un proceso lineal, existen técnicas, como la de tomar logaritmos, que permiten el ajuste a otras funciones.
Fundamentalmente son cuatro:
Función exponencial: Se usa para crecimientos y decrecimientos en los
que la tasa es proporcional al valor actual (de forma aproximada). Cuanto mayor
es el valor actual, mayor es el incremento que sufre.
Función logarítmica: Si se da la proporcionalidad anterior entre el valor
actual y la tasa, pero de forma inversa, es decir, que la tasa de variación sea
proporcional al valor inverso del actual (1/X), el mejor ajuste es el
logarítmico.
Función potencial: Es la más potente, pues permite encontrar un exponente
fraccionario, lo que abarca las potencias y raíces de todo tipo de exponentes.
Su expresión es y = a.xb
Función polinómica: Suelen ajustarse bien a los datos, pero sus fórmulas pueden complicarse.
|
|
En el resumen teórico dispones de una explicación más detallada de la regresión no lineal. |
En LibreOffice.org están contenidos directamente los tipos exponencial, potencial, lineal y logarítmico. Para este curso se ha construido también un ajuste cuadrático. Los ajustes polinómicos requieren cálculos matriciales y no se incluyen aquí.
Abre la hoja tendencias.ods y ajusta con él estos datos:
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Y | 1 | 3 | 6 | 7 | 10 | 13 | 21 | 24 | 35 | 67 | 72 |
Para ello rellena en columna los datos de X e Y, en la primera hoja Entrada de datos, borrando después el resto del área de entrada.
También puedes copiar esta tabla a la hoja Borrador de tendencias.ods, y desde allí usar Copiar, pasar a la hoja de Entrada de Datos y usar Pegado Especial, activando Transponer y eligiendo copiar sólo Números.
Observa los gráficos de la hoja Entrada de Datos. Podemos observar en ellos que el ajuste lineal y el logarítmico no se ajustan bien y tienen un coeficiente bajo. Los ajustes potencial, cuadrático y exponencial son muy buenos, y es difícil distinguir cuál de ellos se ajusta mejor a los datos. Para ello debes estudiar el valor del coeficiente de determinación R2 en cada uno de ellos.
Potencial: R2 = 0,9611 Cuadrático: R2 = 0,9577 Exponencial R2 = 0,9582
Luego, por muy poco, el mejor ajuste lo presenta la función Y´=0,831X^1,714
Independientemente del valor de R2 , podemos tener motivos teóricos para elegir uno u otro ajuste. Por ejemplo, si los datos anteriores correspondieran a ciertos crecimientos biológicos, usaríamos la exponencial.
Otro ejemplo
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Y | 1 | 5 | 10 | 14 | 23 | 40 | 50 | 70 | 80 | 95 |
Repite los pasos y observarás que los mejores ajustes son la potencial y la cuadrática. La elección dependería del modelo previo, si lo hubiera. En caso contrario son determinantes las preferencias de quien realice el experimento.
Además de la hoja tendencias.ods, que agrupa todos los casos de regresión no lineal, puedes consultar cada caso uno a uno en archivos separados:
Exponencial: archivo exponencial.ods
Potencial: Archivo potencial.ods
Logarítmica: Archivo logaritmica.ods
Cuadrática: Archivo cuadratica.ods
Hasta la llegada de los ordenadores a la enseñanza, era muy difícil abordar en la Enseñanza Secundaria ajustes no lineales en tablas de datos procedentes de trabajos de campo o experimentos. Con la Hoja de Cálculo podemos intentar descubrir propiedades aunque los cálculos en que se basan tengan que dejarse a las herramientas informáticas. Como lo importante es la comprensión de conceptos y procesos, no sería muy grave prescindir de los cálculos.
Esta situación se produce, por ejemplo, al comparar medidas múltiples realizadas en Biología sobre un organismo. Al escribir los datos en una hoja de cálculo se podrán descubrir relaciones alométricas que de otra forma pasarían desapercibidas.
Un caso práctico de este tipo lo tienes en el documento ampliar52.pdf
Cambios en la resistencia eléctrica según la temperatura
La resistencia (en realidad, la resistividad) de un conductor metálico aumenta o disminuye según aumente o disminuya también la temperatura. La relación entre ambos cambios se mide con coeficiente a, que se define como el cambio de resistividad por cada grado centígrado de variación.
La fórmula que relaciona estas magnitudes es
Rt = R0*(1+a∆t)
siendo R0 la resistencia inicial de un conductor metálico, Rt la final si se cambia la temperatura, a el coeficiente de cambio de resistividad y ∆t el incremento de temperatura en º C
Es interesante evaluar el valor de a a partir de un experimento. Puedes seguir un desarrollo en el documento ampliar53.pdf