 |
|
|
|
|
|
Divisibilidad Teoría Propuestas Diccionario Herramientas
Divisibilidad Teoría Propuestas Diccionario Herramientas |
Estás en Inicio > Sin decimales > Divisibilidad > Propuestas
Divisibilidad
Propuestas
Dentro de estas propuestas encontrarás búsquedas, ejercicios, demostraciones, etc. ordenadas según los siguientes temas:

Uso del Buscador de Naturales en la Enseñanza Media
![]()
Comprobación de fórmulas clásicas para obtener números primos
Descomposición de primos en suma de cuadrados
![]()
Cuestiones sobre múltiplos y divisores
Las rutas de los números
primos
Colección de propuestas inspiradas en la
espiral de Ulam
![]()
![]()
Problemas de concursos y olimpiadas matemáticas.
![]()
Practica la teoría emprendiendo algunas demostraciones
![]()
Calcular A y B dados el MCD(A,B) y el MCM(A,B)
Números compuestos consecutivos
Si deseas conseguir un conjunto de n números compuestos consecutivos, es decir, sin ningún número primo en el conjunto, basta que uses la secuencia:
(n+1)!+2, (n+1)!+3, (n+1)!+4, …(n+1)!+5....
Con el Buscador de Naturales puedes usar la condición NO ES PRIMO entre esos límites o alguno más amplio y comprobar que todos son compuestos. En la figura se exige que N no sea primo y se busca entre 7! y 7!+11 (como ejemplo)
Como 7!=5040, se comprueba que son compuestos desde 5040 hasta 5050.
Igualmente, plantea una búsqueda de compuestos entre 720 y 730.
Encuentra, finalmente, una secuencia de 12 compuestos consecutivos.
Estos resultados nos prueban que existen números primos consecutivos cuya diferencia es tan grande como deseemos.
Esto tiene otra consecuencia:
"Ninguna fórmula del tipo f(n)=an+b puede representar todos los números primos".
Recuerda antes lo que son números primos gemelos.
Esta búsqueda es muy sencilla: o usas una tabla de números primos, o con el Buscador de Naturales planteas una búsqueda con estas condiciones:
PRIMO ES PRIMO(N+2) EVALUAR N+2 La primera exige que N sea primo. La segunda que lo sea N+2 y la tercera escribe el valor de N+2 junto al de N
Con estas condiciones obtendríamos números primos gemelos. En la imagen puedes ver el resultado del 3 al 100
Núm. Solución Detalles 1 3 5 2 5 7 3 11 13 4 17 19 5 29 31 6 41 43 7 59 61 8 71 73
Reciben este nombre los números primos p tales que 2*p+1 también es primo: 2, 3, 5, 11, 23, 29, 41, 53, 83, 89,...
Usa el Buscador de Naturales.
PRIMO ES PRIMO(2*N+1) EVALUAR 2*N+1 Sólo existe un número N de Sofie Germain que tenga tres cifras, sea capicúa y su pareja 2*N+1 también sea capicúa ¿De qué número se trata?
Sólo tienes que añadir una declaración y una condición nueva. La solución es N=191 y 2N+1=383
Indicadores de Euler de números consecutivos
1) Busca un número N cuyo indicador de Euler (cuenta los números inferiores a N que son primos con él, incluido el 1) es la suma de los indicadores de N+1 y de N+2
Usa una declaración y la función EULER. (La solución tiene tres cifras)
2) Ahora busca otro M cuyo indicador es cuatro veces mayor que el de M+1. (También tiene tres cifras)
Sabemos que dados dos números a y b primos entre sí, existirán dos números enteros x e y tales que se cumpla x*a+y*b=1, y, por tanto, existirán otros dos m y n tales que m*a+n*b=N, siendo N cualquier entero positivo.
La cuestión que planteó Frobenius (problema de las monedas) es para qué números enteros no negativos estos números m y n pueden ser también no negativos, o existirá alguno en el que esto sea imposible. Por ejemplo, 5m+7n nunca es igual a 23 si m y n son mayores o iguales a cero. Esta misma cuestión se puede plantear para tres, cuatro o más números.
Este problema es llamado también de las monedas, porque equivale a discutir si una cantidad de dinero se puede expresar sólo con dos o tres tipos de monedas.
Se puede demostrar que para números grandes siempre es posible esta expresión de un número como suma de dos o más múltiplos de otros que sean primos entre sí. Existirá, por tanto, un número que sea el mayor para el que no se cumpla. Este es el llamado número de Frobenius, y encontrarlo para un conjunto de varios números primos entre sí es un problema muy complejo.
Con el Buscador de Naturales es posible encontrar fácilmente este número para dos, tres o cuatro números primos entre sí en los casos sencillos.
Por ejemplo, intentemos encontrar el número de Frobenius para 5 y 7.
Para ello borra todas las condiciones y activa la de suma espacial. Escribe M5 (múltiplo de 5) en el primer sumado y M7 en el segundo. Así:
Núm. Solución Detalles 1 5 5 + 0 2 7 0 + 7 3 10 10 + 0 4 12 5 + 7 5 14 0 + 14 6 15 15 + 0 7 17 10 + 7 8 19 5 + 14 9 20 20 + 0 10 21 0 + 21 11 22 15 + 7 12 24 10 + 14 13 25 25 + 0 14 26 5 + 21 15 27 20 + 7 16 28 0 + 28 17 29 15 + 14
Buscamos desde el número 1 Hasta el número 36 Con estas propiedades: SUMA M5 M7 Activa la búsqueda de números y comprueba que el número de Frobenius para 5 y 7 es el 23.
Actividad
Busca el número de Frobenius para varios pares de números primos entre sí. Recoge los resultados en una tabla e intenta encontrar una ley de formación.
Comprueba tu resultado investigando páginas web que traten del tema, y lo podrás comprobar con la solución que encontró Sylvester.
Experimenta con ternas de números primos entre sí, aunque este caso es más difícil.
![]() Fórmulas
para obtener números primos
Fórmulas
para obtener números primos
Si deseas comprobar hasta qué número son válidas las fórmulas que generan números primos, puedes usar el Buscador de Naturales. Por ejemplo, para comprobar la fórmula n2+n+17, que fue muy popular en su tiempo, puedes usar estas condiciones:
| CUADRATICO 1 1 17 |
| EVALUAR PRIMO(N) |
y observarás que obtienes números primos que dependen de N=1, N=2, etc. en los que el resultado es 1, porque son primos, hasta n=15 y que después falla en N=16 y N=17 en los que el resultado es 0: el 289 y el 323, ambos divisibles entre 17 ¡Pero eso era de esperar! ¿Por qué?
| Núm. | Solución | Detalles |
| 1 | 19 | 1 |
| 2 | 23 | 1 |
| 3 | 29 | 1 |
| 4 | 37 | 1 |
| 5 | 47 | 1 |
| 6 | 59 | 1 |
| 7 | 73 | 1 |
| 8 | 89 | 1 |
| 9 | 107 | 1 |
| 10 | 127 | 1 |
| 11 | 149 | 1 |
| 12 | 173 | 1 |
| 13 | 199 | 1 |
| 14 | 227 | 1 |
| 15 | 257 | 1 |
| 16 | 289 | 0 |
| 17 | 323 | 0 |
![]() Comprueba de la misma forma que 2n2+9
produce primos desde n=1 hasta n=8 y que n2-n+41,
es válida de n=1 a n=40
Comprueba de la misma forma que 2n2+9
produce primos desde n=1 hasta n=8 y que n2-n+41,
es válida de n=1 a n=40
En toda sucesión aritmética a+b.n con a y b primos entre sí existen infinitos números primos.
Podemos comprobarlo (parcialmente) con una sucesión concreta, por ejemplo con 5*n+7. Basta pedir al Buscador de Naturales que encuentre, entre 1 y 3000 (por ejemplo), los números que cumplen
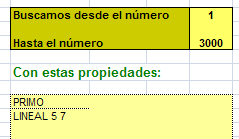
y ver que no dejan de aparecer primos. Y todos terminan en 7. Investiga la causa.
Te proponemos una investigación: ¿Depende mucho la proporción de primos que aparecen del rango de búsqueda o de los coeficientes de la sucesión aritmética?
![]() Teorema
de la descomposición de números primos en sumas de cuadrados
Teorema
de la descomposición de números primos en sumas de cuadrados
Todo número primo del tipo 4n+1 se puede descomponer en suma de dos cuadrados, pero ninguno de la forma 4n+3 admite esa descomposición.
Para comprobar este teorema, fija un intervalo de búsqueda amplio, por ejemplo del 1 al 100. Concreta las condiciones de ser primo y admitir la descomposición de la forma 4n+1. En el Buscador de Naturales las condiciones tendrían esta forma:
| PRIMO |
| LINEAL 4 1 |
En el intervalo de 1 al 100 obtendríamos los números 5, 13, 17,...89, 97. Si ahora añadimos la condición de ser suma de cuadrados, deberán resultar los mismos números. En efecto, añadimos la condición SUMA C C, sin borrar las condiciones anteriores:
| PRIMO |
| LINEAL 4 1 |
| SUMA C C |
y obtenemos los mismos números 5, 13...97, con lo que queda comprobado el teorema.
Para comprobar la segunda parte, basta cambiar los coeficientes 4 y 1 de la fórmula lineal por 4 y 3, y comprobaremos que no se obtiene ningún resultado, debido a la imposibilidad de cumplir las tres condiciones de ser primo, tener la forma 4n+3 y ser suma de cuadrados de forma simultánea.
¿Qué tipo de divisores tiene n!+1 o n!-1? Generalizar
Puedes intentar pensar en la cuestión contraria: qué divisores no pueden tener.
Te puede ayudar el Buscador de Naturales. Por ejemplo, plantea las búsquedas de divisores de FACT(8)+1 o de FACT(10)-1
Para implementarlo en el buscador puedes rellenar una de las celdas vacías con la fórmula =fact(8)+1 o con la fórmula =fact(10)-1 y después pedir los divisores de ese número.
Una curiosidad
Todo número tiene un múltiplo de la forma 1111…1000…0.
En efecto, si tomamos los n+1 números 1, 11, 111, 1111, …, 11111…(n+1….1, al dividir cada uno entre n se producirán n+1 restos, luego alguno estará repetido. Basta entonces restar los dos números que producen el mismo resto.
Otra curiosidad
Esta propiedad es muy conocida: todo número que se pueda escribir como dos grupos iguales de tres cifras, como 234.234, 876.876, etc., se puede dividir exactamente entre 7, el cociente obtenido entre 11 y el siguiente cociente entre 13, con un resultado curioso
¿Qué resultado es ese? Si divido 543543 entre 7, después entre 11, y por último entre 13 ¿qué me resulta?
¿Por qué ocurre eso?
Ocurre igual con números escritos mediante dos grupos iguales de cuatro cifras, como 36.543.654, pero ahora no hay que usar 7, 11 y 13, sino otros números más grandes ¿Cuáles?
Número de divisores
1) Inventa números con sólo tres divisores propios. Ídem con 4.
2) Encuentra un tipo de números N en los que la suma de los divisores propios de N sea igual a N-1
(Puedes obtener una pista si en el Buscador de Naturales escribes SUMDIV(N) en el Evaluador)
El número 945 es el más pequeño que cumple ser Abundante e Impar. ¿Cuál es el siguiente?
Usa el Buscador de Naturales y elige adecuadamente dos condiciones elementales.7
97
397
9397
39397
739397
73939
7393
739
73
77
37
137
9137
29137
629137
7629137
67629137
567629137
6567629137
16567629137
216567629137
6216567629137
46216567629137
646216567629137
2646216567629137
12646216567629137
312646216567629137
6312646216567629137
86312646216567629137
686312646216567629137
7686312646216567629137
57686312646216567629137
357686312646216567629137
31
331
3331
33331
333331
3333331
33333331
7
73
739
7393
73939
739391
7393913
73939133
La dificultad de cada demostración viene dada por el número de "pizarritas":
Fácil
De tipo medio
Difícil
Las demostraciones requieren un cierto nivel de conocimientos, pero siempre son asequibles a los aficionados al tema. No son propias de profesionales.
Demuestra que todo número primo mayor que 3 es de la forma 6n+1 o de la forma 6n-1
Ayuda: Piensa que todos los números tienen una de estas seis formas: 6n, 6n+1, 6n+2, ... 6n+5 y cuáles dan lugar a números compuestos.
Consecuencia: Demuestra que el número natural comprendido entre dos números primos gemelos mayores que 3 es múltiplo de 6.
Otra: No puede existir una terna de números gemelos mayores que 3 (sólo existe 3, 5, 7), es decir, tres números de la forma p, p+2 y p+4 que sean los tres primos.
Y otra: El cuadrado de un número primo mayor que 3 tiene la forma de múltiplo de 12 más 1.
Demuestra que si m.c.d(a,b) = 1, se verificará que m.c.d(a+b,a-b) será igual a 1 o a 2
Demuestra que si el número 3 divide a un cuadrado perfecto n2, necesariamente ha de dividir a n.
Ayuda: Considera el número n escrito como 3m+k
Demuestra que todo número cuadrado perfecto tiene un número impar de divisores.
¿Podrías demostrar lo que se afirma en la comprobación primera?
Para todo N, existe una serie de N números compuestos consecutivos.
Ayuda: Piensa que (N+1)! es divisible entre 2,3,4...N ¿Entre qué números serán divisibles cada uno de los elementos de esta secuencia?
(n+1)!+2, (n+1)!+3, (n+1)!+4, …(n+1)!+5....
¿Podrías demostrar el criterio recursivo para saber si un número es múltiplo de 7?
Para ver si un número es divisible entre 7 se apartan su última cifra de la derecha, se multiplica por 2 y se resta el resultado del resto de número formado por las cifras que quedan. Si se obtiene un número múltiplo de siete, el número primitivo también lo es. Podemos probarlo con el número 191548, que se transforma en 19154 - 2*8 = 19138. Si no sabemos si es múltiplo de 7, reiteramos la operación: 1913 - 2*8 = 1897, Podemos continuar: 191 - 2*3 = 175, que es múltiplo de 7 por ser 7*15. Según este criterio, también será múltiplo de 7 el primitivo número.
Ayuda: Representa el número como 10*A + B, donde B es la última cifra y 10*A el número al quitarle esa última cifra. La operación propuesta en el criterio es A - 2B, que si el número resultante es múltiplo de 7, se podrá escribir: A - 2B = 7M, siendo M un número adecuado. El resto de la demostración es cosa tuya.
Variante: Demuestra que todo número primo mayor que 2 es de la forma 4n+1 o de la forma 4n-1
Todo número de la forma n2-1 es múltiplo de 8 si n es impar.
Ayuda: Recuerda cómo se descompone en factores el polinomio n2-1
Encuentra un conjunto de valores de n tales que 2n - 1 sea múltiplo de 7
Ayuda: Al factorizar n, también se factoriza 2n - 1
Nueva (adaptación de una propuesta de Henri Camous)
Elige un número de tres cifras abc, forma los seis números que contienen las mismas cifras, pero en otro orden bca, cab, etc. (por ejemplo 345, 543, 354, ...) Suma esos seis números. Siempre obtendrás un múltiplo de 222. Demuéstralo.
Ayuda: Escribe abc como 100a+10b+c. Haz lo mismo con los demás.
Demuestra que todo número perfecto par termina en 6 o en 8
Ayuda: Consulta la teoría de los números perfectos y la fórmula encontrada por Euclides. ¿En qué cifras pueden terminar los números del tipo 2n y los del tipo 2n-1?
Demuestra que ningún número natural que se exprese mediante la fórmula n4 + 4 es primo, salvo el número 5
Ayuda: Suma y resta 4n2 e intenta factorizar la expresión resultante.
Demuestra, como hizo Euclides, que si el número 2k-1 es primo (número de Mersenne), el número N=2k-1(2k-1) es perfecto.
Ayuda: Si llamas p al número 2k-1, los únicos divisores de N serán 2 y p, y basta aplicar la fórmula de la suma de divisores a la descomposición N=2k-1.p (recuerda que N no entra en la suma)
Demuestra que todo número de la forma n3 + 5n, con n natural, es múltiplo de 6
Ayuda: Usa el principio de inducción completa. Es evidente que se cumple para n=1.
Todo múltiplo de 6 mayor que 6 es abundante
Ayuda: Si es múltiplo de seis, poseerá una mitad, una tercera parte y una sexta, al menos, que sean enteras. Eso te dará una pista.
Todo número de la forma 2n-1 con n compuesto, es también compuesto.
Además, puede ser descompuesto en dos factores que son sumas de potencias de 2 cuyos exponentes están en progresión aritmética.
Ayuda: Recuerda que el polinomio an-1 se descompone en dos factores, uno de los cuales es a-1. Si a es 2, no ganamos nada, porque a-1 valdría 1. Pero si n es compuesto y recuerdas la las formas de escribir la potencia de otra potencia podrás lograr algo.
(Propuesta por Paul Erdös) Si tomamos n+1 números naturales cualesquiera, todos ellos menores que 2n. entre ellos habrá al menos dos que sean primos entre sí.
Ayuda: Basta tener en cuenta una condición suficiente muy conocida para que dos números naturales sean primos entre sí ¿cuál?
Existen infinitos primos que siguen la fórmula 4n+3
Ayuda: Considera que todos los números primos tienen la forma 4n+1 o 4n+3. Si de estos últimos no hubiera infinitos, existiría un N=4k+3 que sería el último primo de esa clase. Usa un razonamiento similar al de Euclides para demostrar que sería falso, que habría un primo del tipo 4n+3 mayor que él.
Ningún primo que siga la fórmula 4n+3 se puede descomponer en suma de cuadrados.
Ayuda: Considera si los sumandos son pares o impares y descubrirás que la suma puede tener las formas, 4n, 4n+1 o 4n+2, pero nunca 4n+3
Dos números triangulares consecutivos mayores que 1 no pueden ser nunca primos entre sí. Es más, podemos siempre tener una idea de qué factores comunes podrán presentar.
Ayuda: Un camino rápido es recordar la fórmula del número triangular Tn
Problemas de competiciones y olimpiadas
El número A3640548981270644B es divisible por 99. Calcula A y B
Si aplicas los criterios de divisibilidad por 9 y por 11 llegarás a un sistema de ecuaciones con soluciones A=9 y B=1
¿Cuál es el entero N más pequeño cuyo factorial N! termina en 25 ceros?
Para conseguir 25 ceros necesitarás disponer de factores 2 y 5. El 2 no presenta problema, porque los números pares son muy abundantes. Deberás contar múltiplos de 5. La solución es 105.
Siendo p un número primo, encuentra las soluciones enteras de la ecuación p(x+y) = x.y
El número p divide al producto x.y, luego divide a x o divide a y. De ahí sacas una consecuencia inmediata, que te lleva fácilmente a las soluciones
0 y 0, 2p y 2p, p(p+1) y p+1, p(1-p) y p-1, además de sus simétricas.
Demostrar que existe una sucesión de números a1, a2, a3, ....an, ...tal que las sumas de cuadrados del tipo
a12 + a22 + a32 + ....an2 son cuadrados perfectos para cualquier valor de n.Nos piden una demostración de existencia, luego basta con presentar una. Podemos comenzar con 32 + 42, que equivale a 25, que es cuadrado perfecto. Si el 25 y las sucesivas sumas las hacemos equivalentes a una diferencia de cuadrados (con ciertas condiciones), tendremos la solución. Analiza los cálculos que se han efectuado con hoja de cálculo (sólo figuran los primeros términos, pero se podrían seguir produciendo cuadrados perfectos.:
Uso de la hoja de cálculo:
Sucesión Cuadrado Suma cuadrados Es cuadrado perfecto 3 9 9 3 4 16 25 5 12 144 169 13 84 7056 7225 85 3612 13046544 13053769 3613 6526884 42600214749456 42600227803225 6526885
¿Qué números de dos cifras al dividirlos entre la suma de las mismas dan como cociente el número 7?
Tienes dos caminos: O bien recorres los múltiplos de 7 o bien representas el número como 10a+b. Es fácil llegar a que a=2b y que las soluciones son 21, 42, 63 y 84.
¿Quieres comprobarlo con el Buscador de Naturales?
Encuentra todas las ternas x, y, z de números primos que cumplen xy + 1 = z
Las condiciones de paridad de los tres números hacen que la única terna posible sea x=2, y=2, z=5. La parte más complicada es razonar que y debe ser par.
Se disponen de forma aleatoria los números 1,2,3,4,5,6,7,8 y 9 en una tabla de tres filas y tres columnas.
A continuación se suman los seis números de tres cifras que resultan agrupando por filas y por columnas.
En el ejemplo sería 365+297+148+321+694+578
Demuestra que esa suma siempre será un múltiplo de 9, para cualquier ordenación de los nueve números.
3 6 5 2 9 7 1 4 8 Debes tener en cuenta que 100=99+1 y 10=9+1. Parece poca ayuda, pero es suficiente.
Siendo p un número primo distinto de 2 y de 5, existen infinitos números del tipo 1111111...111, escritos en base 10, que son múltiplos de p.
Deberás conocer la congruencia de Fermat, lo que te permitirá demostrarlo para números del tipo 99999...99999. El paso posterior a los del tipo 11111...11111 es más fácil.
Otra forma de abordarlo es la de demostrar previamente que la suma de los p-1 primeros restos potenciales de 10 respecto de cualquier número primo p es un múltiplo de p. Así, por el criterio general de divisibilidad, mediante restos potenciales (ver teoría de las congruencias) consigues fácilmente la demostración
Uso de la hoja de cálculo:
La propiedad que se usa en el segundo método la puedes comprobar con las herramientas potenciales.ods y potenciales.xls
¿Para qué valores de k y p la raíz cuadrada de k2 - kp es un número entero, si k ha de ser entero y p un número primo?
Una forma de abordarlo sería igualar k2 - kp a un cuadrado m2, resolver la ecuación correspondiente en k y exigir que el discriminante sea también un cuadrado perfecto. Es un camino laborioso, pero se logra.
Otra forma sería considerar el producto k(k-p) y estudiar cómo se reparten los factores primos para conseguir un cuadrado perfecto. También es laborioso, pero se llega a la misma conclusión.
Las soluciones son: k=0, k=p, k=((p+1)/2)2 y k= - ((p-1)/2)2
Construye un modelo de Hoja de Cálculo que resuelva esta cuestión:
Dado un número natural N y otros dos a y b menores que él, ¿cuántos números naturales existen que no sobrepasen N y que no sean múltiplos ni de a ni de b?
Necesitarás muy pocas fórmulas, pero las adecuadas. Puedes comprobar tus resultados con el Buscador de Naturales.
Te damos algunas soluciones para que compruebes:
Si N=400, a=45 y b=28 resultan 378 números
Para N=300, a=20 y b=18 resultan 270 números
Una experimentación: Dados el MCD(A,B) y el MCM(A,B), encontrar A y B Nueva
Esta propuesta está basada en una cuestión desarrollada por Pablo Rey Villaverde (1943).
Escribe en una hoja de cálculo los dos valores, por ejemplo MCD(A,B)=5 y MCM(A,B)=455.
Realiza los cálculos oportunos (has de usar una propiedad conjunta del MCD y el MCM) y resultará una solución única:
A=65 y B=35
Usa las funciones M.C.D y M.C.M de la hoja de cálculo para comprobar.
Haz lo mismo con MCM(A,B)=24360 Y MCD(A,B)=15. En este caso existirán tres soluciones.
¿De qué depende el número de soluciones posibles?
Resuelve algunas cuestiones parecidas y construye en la hoja tablas
ordenadas con todas sus soluciones.