|
|
|
|
|
|
|
Estás en Inicio > Sin decimales > Divisibilidad > Rutas de los números primos
Rutas rectangulares
Hoja de cálculo Rutrectrang
Descripción de la hoja
Esta hoja clasifica los números naturales según una tabla rectangular, en la que las columnas representan conjuntos de números congruentes respecto al módulo representado por el número de columnas.

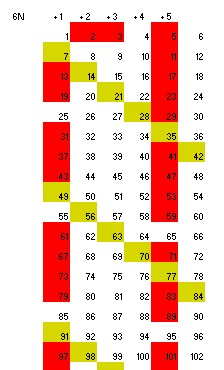
Como ejemplo, en la imagen, diseñada para seis columnas, se puede observar que los números primos, salvo los iniciales, están situados en las columnas congruentes con 1 y con 5 módulo 6.
Los controles de la hoja son muy simples.
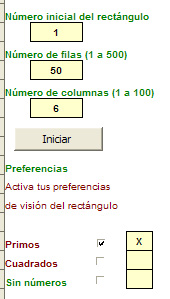
Se pueden fijar el número inicial del esquema que, salvo indicación contraria, se supondrá que es el 1, y el número de columnas y de filas. Este último no deberá ser muy grande, salvo necesidades de alguna experimentación, porque ralentiza la construcción de la tabla.
Las preferencias se fijan activando los distintos tipos de números que se deseen estudiar: primos, cuadrados, múltiplos, etc.
Con el botón Iniciar se comienza la construcción de la tabla
Sobre este esquema plantearemos las siguientes cuestiones, según el número de columnas
Son cuestiones sencillas, muchas de ellas simples comprobaciones, pero que pueden ser útiles para repasar algunos conceptos y propiedades, y entretenidas para el alumnado
Dos columnas:
Fija en 2 el número de columnas para seguir las explicaciones

Este esquema divide a los números en pares e impares. Lo único que es posible destacar n él es que todos los números primos (salvo el 2) caen en la columna de los impares.
También se destacan los números primos gemelos, como pequeños rectángulos formados por dos cuadraditos. En la imagen se pueden ver las parejas 3 y 5, 5 y 7, 11 y 13, 17 y, por último, 29 y 31.
Propuestas:
¿Cuántos pares de primos gemelos existen entre 1 y 100? (Sol. 8)
![]()
Ver propuesta similar con el Buscador de Naturales
¿Cuál es la distancia máxima entre dos pares consecutivos en ese intervalo? (Sol. 18)
Extiende estos cálculos a otros intervalos. Saca consecuencias empíricas
Busca
cuatripletes
de primos gemelos, es decir, dos parejas de primos gemelos que estén lo más
cercanas posible, como 11,13,17 y 19 o bien 101,103,107 y 109.
Observa que la mínima distancia entre parejas es 4. No puede ser menor ¿por qué?
Busca más conjuntos similares. Hasta 1000 se encuentran dos más.
Tres columnas:
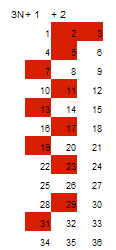
Si se fija el número de columnas en 3, es evidente que los números primos sólo figurarán en las columnas 3n+1 y 3n+2, puesto que no pueden ser múltiplos de 3, salvo el mismo 3.
No hay dos primos contiguos en una misma columna. Siempre queda al menos un hueco entre ellos. ¿Cuál es la razón?
Un ejercicio lúdico que puede dar juego, es el de buscar "cremalleras", como las de la figura , que están formadas por 7, 11, 13, 17, 19, 23
Propuestas:
Escribe la expresión algebraica de cuatro primos (o más) seguidos en forma de cremallera (Sol por ejemplo, 3n+1,3n+5,3n+7,3n+9,3n+11, etc... Se ve que forman una sucesión en la que las diferencias se alternan entre 2 y 4)
Busca "uves" y "uves dobles formadas por primos" ¿Qué expresiones siguen estos conjuntos de números?

| Busca estructuras con simetría axial, como esta. Busca alguna expresión para ellas.
|
 |
Cuatro columnas:
Este caso presenta mucho interés, porque se estudiaron mucho los conjuntos de primos de la forma 4n+1 y 4n+3
En primer lugar observa que las columnas que contienen primos son precisamente estas: 4n+1 y 4n+3

.
Propuestas:
Según un teorema clásico, todos los números primos de la forma 4n+1 se pueden descomponer en suma de cuadrados. Comprueba esta propiedad en la columna correspondiente, buscando directamente su descomposición en suma de dos cuadrados: 5 = 4 + 1, 13 = 9 + 4, 17 = 16 + 1, 29 = 25 + 4,...
Intenta ahora la comprobación con la ayuda del Buscador de Naturales
Para ello abre el Buscador de Naturales (ver las Herramientas de Divisibilidad)
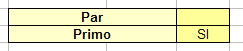
Borra todas las condiciones y define los números buscados como primos de la forma 4n+1
Para ello activa la condición lineal 4n+1

y la de ser primo
De esta forma, obtendrás, por ejemplo los primos de este tipo existentes en el intervalo 1...100
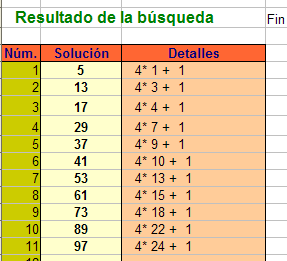
Toma nota de los números primos resultantes y añade, sin borrar ninguna condición, la condición de ser suma de cuadrados
Vuelve a iniciar la búsqueda y obtendrás los mismos números primos, esta vez expresados como suma de cuadrados, con lo que queda comprobado el teorema.
También se demuestra que los números primos de la forma
4n+3 no se descomponen nunca como suma de cuadrados.
Repite la propuesta anterior, cambiando 4n+1 por 4n+3 y obtendrás la
comprobación.
En efecto, no se encuentran descomposiciones en suma de cuadrados para 7, 11, 19, 23, ...
Con el Buscador se percibe la imposibilidad de forma muy clara. Cambia la condición 4n+1 por 4n+3 y define el número como primo y como suma de cuadrados. Busca en un intervalo grande, como de 1 a 2000, y no obtendrás ningún resultado en la búsqueda.
Número superior de columnas
Casos particulares
En el caso de 6 columnas se puede comprobar que todos los primos son de la forma 6n+1 o 6n+5, porque a partir del 5 sólo se rellenan de primos estas dos columnas.
Con 8 columnas se puede verificar que nunca hay cuatro primos en la misma fila, ni siquiera tres seguidos (de 2 en 2) ¿Cuál es la causa?
Si fijamos 10 columnas se situarán verticalmente,
unos debajo de otros, los números primos que terminan en la misma cifra, que es,
evidentemente, 1, 3, 7 y 9 (salvo el 2 y el 5).
También podemos observar muchos números primos consecutivos, en el sentido de
diferenciarse en 10 unidades y terminar, por tanto, en la misma cifra. Así
aparecen las parejas 73 y 83, 139 y 149, etc. ¿Por qué no
parecen tríos de números primos que aparezcan de 10 en 10 terminando en la misma
cifra?
Caso general
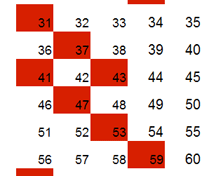
Para números impares surgen escaleras (números primos en sucesión aritmética de diferencia igual al número de columnas más o menos una unidad). Se pueden buscar escaleras con el máximo de tramos posible, como la de la figura:
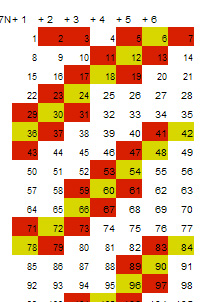
La búsqueda de escaleras se puede "adornar" si
además de números primos se piden múltiplos de 6. Buca en los controles la forma
de hacerlo.
¿Por qué resultan estas figuras?
Al igual que las escaleras de primos, aparecerán otras de compuestos. Dependerá del número de columnas. Por ejemplo, en el caso de 6, las diagonales avanzarán de 5 en 5 o de 7 en 7, según su orientación. En el caso de 5, se formarán diagonales sin primos formadas por múltiplos de 5. Igual ocurre con el 7 (ver la segunda imagen)
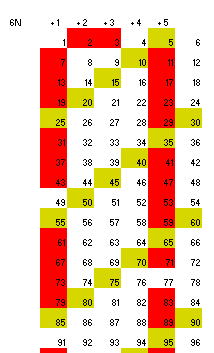
Experimenta con otros números de columnas N y observa los múltiplos de N+1 o de N-1. Prueba también con los múltiplos de los divisores de esos dos números. En algunos caso obtendrás enrejados muy tupidos
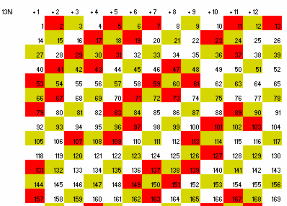
También aparecen rombos, romboides, etc. que pueden ser materia de investigaciones o alguna competición.
Para números pares todos los primos aparecen en columna, y no se producen estas figuras.
También se puede comprobar que los números primos no dejan de aparecer en las columnas cuyo ordinal es primo con el número de columnas. Esto es consecuencia del teorema de Dirichlet: En toda sucesión aritmética a+b.n con a y b primos entre sí existen infinitos números primos. Por ejemplo, en el caso de ocho columnas, aparecerán infinitos primos en las columnas 8N+1, 8N+3, 8N+5 y 8N+7 y en el caso de 12, habrá infinitos en 12N+1, 12N+5, 12N+7 y 12N+11. En el resto de columnas no hay primos ¿Por qué?
¿Valdría este hecho para encontrar el Indicador de Euler de un número por simple conteo?