Aritmética Teoría Propuestas Herramientas
Estás en Inicio > Sin decimales > Aritmética > Diccionario
![]() Descarga
en PDF (No funcionarán los enlaces externos)
Descarga
en PDF (No funcionarán los enlaces externos)
Pequeño diccionario de Aritmética
Se incluyen también algunos conceptos de teoría de conjuntos.
Selecciona una letra o un tema:
A
Valor absoluto
El valor absoluto de un número real se define como él mismo si es positivo o cero, o su opuesto si es negativo. Se representa con el símbolo |n|
Si n>=0, |n|=n Si n<0, |n|=-n
Sinónimo de conmutativo.
Es la operación de sumar dos números.
Aunque se usa también en otros sentidos, se llama número afortunado al que sobrevive a una criba. Por ejemplo, los números primos son afortunados para la criba de Eratóstenes.
Es una serie finita de reglas o cálculos en un orden determinado para obtener un resultado a partir de unos datos
Algoritmo de la numeración
Conjunto de reglas y convenios que permiten, dada una base de numeración, representar cualquier número mediante un conjunto de símbolos llamados cifras.
Algoritmo 196
Consiste en ir sumando cada número natural expresado en el sistema decimal con el formad con las mismas cifras invertidas. Esta operación se repite hasta desembocar en un capicúa. Por ejemplo: 337+733=1070; 1070+0701 = 1771, que es capicúa. Existen números, como el 196, para los que aún no se sabe si la iteración termina en un capicúa o no. Son los llamados números de Lychrel: 196, 295, 394, 493, 592
Dos números naturales son anagramáticos si las cifras de uno son anagramas de
las del otro, es decir, ambos tienen las mismas cifras (contando repetidas) pero
en distinto orden. Por ejemplo, 151047 y 104571.
Estructura algebraica formada por un conjunto dotado de dos operaciones (las llamaremos suma y producto) tales que se cumple:
El
conjunto para la suma constituye un grupo
aditivo
El producto convierte al conjunto en semigrupo
multiplicativo
El producto es distributivo
respecto a la suma.
Aritmética
Es la ciencia que estudia las operaciones básicas con números racionales. Como tal ciencia se considera fundada por Pitágoras.
Triángulo aritmético
Nombre dado también al triángulo de Pascal o Tartaglia.
Sucesión o progresión aritmética
Es aquella en la que cada término es igual al anterior sumado con un número constante llamado diferencia. Su fórmula de recurrencia es: a1=a; an=an-1+d, donde a (valor inicial) y d (diferencia) son constantes.
Media aritmética
Ver
Media
Un número armónico Hn es un número racional formado mediante la suma de los inversos de los números naturales hasta n, es decir
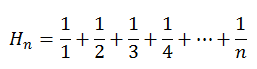
La sucesión de los números armónicos tiene límite infinito, por ser divergente la serie armónica a la que pertenecen los sumandos. Es fácil ver que los denominadores de los números armónicos son, salvo simplificaciones, los primeros factoriales.
Media armónica
Ver Media
Un grupo aditivo totalmente ordenado es arquimediano cuando dados dos elementos del grupo x>0 e y>0, existe siempre un número natural n tal que el producto de x por n (en el sentido de suma repetida) es mayor que y (x*n>y) Se suele expresar coloquialmente como que todos los elementos de ese grupo son alcanzables.
Los números enteros Z son arquimedianos.
Propiedad asociativa
Una operación definida sobre un conjunto se llama asociativa cuando se cumple, para toda terna de elementos a, b y c del conjunto que
(a*b)*c = a*(b*c)
Número automórfico
Un número se define como automórfico cuando su cuadrado tiene como últimas cifras las mismas que ese número. Los primeros números automórficos son 5, 6, 25, 76, 376, 625... En efecto: 52=25, 62=36, 252= 625, 762= 5776, 3762= 141376,...
Para cada número de cifras existen al menos dos números automórficos, uno terminado en 5 y otro en 6.
Es similar al anterior, pero la propiedad la cumple con el cubo: 43 = 64, 243 = 13824, 2493 = 15438249.
Todos los números automórficos son también trimórficos.
Su definición es algo extraña, porque son aquellos números enteros positivos que no pueden ser expresados como la suma de otro entero con la suma de sus cifras. Por ejemplo, 20, no puede generarse con números más pequeños a los que les sumamos sus cifras. Con los de una cifra se ve que es imposible, y con los de dos: 11+1+1=13, 12+1+2=15, 13+1+3=17, 14+1+4=19, 15+1+5=21, y el resto tampoco daría como resultado 20.
Son estos:
1, 3, 5, 7, 9, 20, 31, 42, 53, 64, 75, 86, 97, 108, 110, 121, 132, 143, 154, 165, 176, 187, 198, …
También los puedes estudiar en http://oeis.org/A003052
B
Conjetura de Bachet de Meziriac
Todo número natural puede expresarse como suma de a lo más cuatro cuadrados.
(Fue demostrado más tarde por Lagrange)
Teorema de Bachet de Meziriac
El sistema x2 = y2 + z2 ; y*z=2t2 no tiene solución.
Es decir: "No hay triángulo rectángulo pitagórico con área expresada por un número cuadrado"
Base de un sistema de numeración
Es el número de unidades de orden inferior necesarias para obtener una unidad de orden inmediato superior. Coincide con el número de símbolos necesarios para escribir cualquier número en ese sistema de numeración.
Base de una potencia
Ver Potencia
Estos números han sido introducidos por Eric Angelini y publicados en el año 2005 en http://oeis.org/A106039. Hay varios tipos, por lo que comenzaremos con los 0-Belgas. Estos números tienen la propiedad de que si a partir del número 0 vamos sumando reiteradamente las cifras (por orden) del número dado, se forma una sucesión que contiene a ese número. Por ejemplo, el 18 es 0-belga, porque a partir del 0 vamos a ir sumando sucesivamente 1, 8, 1, 8,…hasta llegar o sobrepasar el 18: 0, 1, 9, 10, 18, resultando que el mismo 18 es término de la sucesión.
Números de Bell
Los números de Bell son los términos de la sucesión 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, ...
Representan las formas de colocar n bolas etiquetadas en n cajas indistinguibles. Por ejemplo, los símbolos a,b y c se pueden situar en tres cajas (eventualmente vacías) de 5 formas: (abc), (a)(bc), (b)(ac), (c)(ab) y (a)(b)(c).
También representan las formas de expresar como producto de factores un número compuesto que equivale al producto de n factores primos distintos. Es el caso del número 30 = 2.3.5 y que también se puede descomponer en producto de 5 formas distintas: 30 = 6.5 = 3.10 = 15.2 = 2.3.5
Ley de Benford
La ley de Benford, también conocida como la ley del primer dígito, asegura que, en los números que existen en la vida real, la primera cifra es 1 con mucha más frecuencia que el resto de los números.
Correspondencia biyectiva
Una correspondencia entre conjuntos se llama biyectiva cuando todos los elementos de uno tienen imagen en el otro y una sola.
Diremos que un conjunto está bien ordenado cuando todo subconjunto no vacío del mismo posee un elemento mínimo.
C
Sinónimo de subconjunto totalmente ordenado. Por ejemplo, los múltiplos de 5 para la relación ≤, o las potencias de 7 para la relación de ser múltiplo"
Sinónimo de palindrómico.
Cardinal de un conjunto
Un número natural n es el cardinal de un conjunto cuando se puede establecer una correspondencia biyectiva entre los elementos del conjunto y los números {1, 2, 3, ... n} Es evidente que si entre dos conjuntos es posible construir una correspondencia biyectiva, tendrán el mismo cardinal. Es una relación que clasifica a los conjuntos en clases de equivalencia.
Producto cartesiano
El producto cartesiano de dos conjuntos A y B es otro conjunto formado por todos los pares posibles formados por un elemento de A y otro de B en ese orden.
Números casi-cuadrados
Son aquellos números naturales que se pueden expresar como n2 - 1. siendo n otro número natural. Por ejemplo, son casi-cuadrados el 8, el 24, el 48, etc.
Números de Catalan
Llamaremos números de Catalan a los términos de la sucesión 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796,...
Ecuación de Catalan
Es la ecuación diofántica xm - yn = 1 con todos x,y,m y n naturales mayores que 1
Conjetura de Catalan
Sólo existe una solución para la ecuación anterior: 32 - 23 = 1
Conjunto cerrado para una operación
Un conjunto es cerrado para una operación (o también, la operación es cerrada en el conjunto) cuando dados dos elementos del conjunto, el resultado de aplicar la operación entre ellos da siempre como resultado otro elemento del conjunto.
Número cíclico
Un número natural de n cifras se llama cíclico cuando al multiplicarlo por cualquier otro número natural entre 1 y n se obtiene un resultado formado por las mismas cifras que él, pero desplazadas cíclicamente.
Por ejemplo, el número 142857 al multiplicarlo por 2 se convierte en 285714 y al multiplicarlo por 3 en 428571. Intenta todos los productos por los números 1, 2, 3, 4, 5 y 6
Cifras en un sistema de numeración
Son los distintos símbolos usados en ese sistema, así 1,2,3...9,0 en el sistema decimal o M,C,D,... en el romano.
Cociente en una división
Ver División
Cociente en una fracción continua
Se toma un número entero positivo N cualquiera, por ejemplo el 13, y se le aplica la siguiente operación, a la que llamaremos función COLL(N):
· Si el número es par, se divide entre 2.
· Si el número es impar, se multiplica por 3 y se le suma 1.
En el caso del 13, como es impar, se le aplicará la segunda, y quedará COLL(13)=13*3+1=40.
La idea de la conjetura es que sigamos aplicando esta operación a todos los resultados que obtengamos, En nuestro caso sería COLL(40)=20 (por ser par), COLL(20)=10, COLL(10)=5, COLL(5)=3*5+1=16, COLL(16)=8, COLL(8)=4, COLL(4)=2, COLL(2)=1, y a partir del 1 se entra en el ciclo {4, 2, 1}
La conjetura afirma que este final en el 1 y el ciclo posterior ocurre para cualquier otro entero positivo. Sea cual sea el comienzo, se llegará al número 1. Todas las sucesiones construidas así terminarán en el ciclo 4, 2, 1.
Una conjetura es una afirmación que parece ser cierta en muchos casos, pero que no se ha podido demostrar.
Propiedad conmutiva
Una operación definida en un conjunto tiene la propiedad conmutativa cuando para todo par de elementos a y b del conjunto se cumple
a*b = b*a
Grupo, anillo o cuerpo conmutativo
Son aquellos en los que es válida la propiedad conmutativa. También se llaman abelianos
Operación de contar
Es la operación de construir una correspondencia biyectiva entre los elementos de un conjunto dado y el conjunto adecuado de los n primeros números naturales. Al valor de n le llamaremos cardinal del conjunto.
La media contraarmónica de un conjunto de números positivos se define como la media aritmética de los cuadrados de los números dividida por la media aritmética de los números. En el caso de dos, a y b, sería (a2+b2)/(a+b)
Convergente de una fracción continua
Es sinónimo de fracción reducida.
Conjuntos coordinables
Dos conjuntos son coordinables cuando se puede establecer una correspondencia biyectiva entre los elementos de uno y otro.
Una correspondencia entre dos conjuntos es cualquier subconjunto de su producto cartesiano. En la práctica consiste en asignar una pareja o varias a todos o algunos elementos del conjunto.
Número cósico
Un número natural a se llama cósico cuando es potencia exacta de otro número natural. Como casos particulares están los números cuadrados, cúbicos, etc.
Números cuadrados
Un número natural a se llama cuadrado cuando existe otro número natural n tal que a=n2.
Cuadrados mágicos
Un cuadrado mágico es una matriz cuadrada de números en la que las sumas por filas, columnas y diagonales son todas iguales.
Número cúbico
Un número natural a se llama cúbico si es la tercera potencia (cubo) de otro número natural.
Cuerpo como estructura algebraica
Un cuerpo es un anillo con elemento neutro para el producto (llamado unidad) en el que todos los elementos salvo el cero (elemento neutro para la suma) poseen un inverso.
Algoritmo de los cumulantes
Es el algoritmo (también se llaman cumulantes los distintos resultados del mismo) que encuentra las reducidas de una fracción continua.
CH
D
Sistema de numeración decimal
Es aquel sistema de numeración posicional en el que cada tipo de unidad (unidades, decenas, centenas, millares, etc.) es diez veces mayor que su inmediata precedente. Sus cifras son 0,1,2,3,4,5,6,7,8 y 9.
Una
sucesión de números naturales puede ser definida por
recursividad. Esta definición se compone de dos
declaraciones:
a) Se definen directamente los valores de los
primeros términos de la sucesión: a1=m,
a2=n, a3=p,...
b) El resto de términos
se define en función de los anteriores an = f(an-1,
an-2, an-3...)
Ejemplo de recursividad es la definición de factorial: 1! = 1, n!=(n-1)!*n o la de la sucesión de Fibonacci: a1=1, a2=1, an=an-1 + an-2
Dada
una sucesión A cualquiera, deberemos conocer una función de conteo a(n),
definida como el número de elementos de A que son menores o iguales a n.
Entonces definiremos la densidad d natural de A (si existe) como el
cociente a(n)/n cuando n tiende a infinito.
Descomposición
Descomposición de un conjunto en sumas
Ver Partición
Desigualdad de números naturales
Un número natural a es menor que otro número b cuando cualquier conjunto del que es cardinal a es coordinable con una parte estricta de otro conjunto cuyo cardinal es b. Si se permite que esa parte pueda ser todo el conjunto, diremos que a es menor o igual que b.
Las relaciones inversas serán mayor y mayor o igual.
Dos números son desiguales si uno de ellos es menor que el otro.
Números de Devlali, autonúmeros o números colombianos.
Son aquellos números enteros positivos que no pueden ser expresados como la suma de otro entero con la suma de sus cifras (Kaprekar llamó a esta operación digitadición).
La diferencia entre dos números a (minuendo) y b (sustraendo), con a mayor o igual que b, es otro número natural c (diferencia) que sumado con b da una suma igual a a.
Número natural de una sola cifra
Ecuación diofántica
Una ecuación diofántica es aquella definida en el conjunto de los enteros, tanto para sus coeficiente como para los valores que puedan tomar las incógnitas.
Sistema diofántico
Es aquel que está formado por ecuaciones diofánticas.
Aproximación diofántica
Es aquella que busca aproximar un número real mediante números racionales. Un ejemplo típico es el de la aproximación a radicales cuadráticos mediante frcciones continuas.
Propiedad distributiva
Una operación * es distributiva respecto a otra operación + cuando se cumple, para toda terna de elementos a,b y c que
a*(b+c) = a*b+a*c
Ver División
División entera
Dados dos números naturales a (dividendo) y b (divisor), llamaremos división entera entre ellos a la operación de encontrar otros dos números naturales q (cociente por defecto) y r (resto por defecto), tales que se cumpla:
a = b.q + r con r<b
Se demuestra que ambos números q y r siempre existen para a y b dados.
También se pueden definir el cociente por exceso y su resto correspondiente:
a = b.(q+1) - r' con r' <b
Se cumple que q + q' = d
Además, si se multiplican por un mismo número natural m tanto el dividendo como el divisor, el cociente no varía, pero el resto queda multiplicado también por m (en ambas modalidades por defecto y por exceso)
División exacta
Dados dos números naturales a (dividendo) y b (divisor), llamaremos división exacta entre ellos a la operación de encontrar otro número q (cociente) tal que se cumpla a=b.q
Si esta operación es posible, diremos que b es divisor de a, o bien que a es múltiplo de b.
Divisor en una división
Ver División
Número divisor de otro
Ver División
E
Ecuación diofántica
Una ecuación diofántica es aquella definida en el conjunto de los enteros, tanto para sus coeficiente como para los valores que puedan tomar las incógnitas.
Ecuación diofántica lineal
La ecuación diofántica de tipo lineal más sencilla es la del tipo Ax+By=C
Para que tenga solución ha de ser C múltiplo de D=MCD(A,B). Se resuelve considerando el teorema que afirma que existen dos enteros m y n tales que mA+nB=D. Los valores de m y n se calculan mediante el algoritmo de Euclides y el algoritmo de las reducidas.
Número equilibrado
Un número es equilibrado en un sistema dado de numeración si (distintas definiciones):
(a) Todos sus dígitos aparecen con la misma frecuencia. Es popular el caso del sistema binario, en el que se exige que aparezcan el mismo número de 1 que de 0.
(b) Aparecen todos los dígitos posibles una vez.
(c) Posee el mismo número de dígitos pares que impares, o bien los pares figuran un número impar de veces y los impares un número par.
(d) Números de tres cifras en las una de ellas es promedio de las otras.
(e)
Los primeros n dígitos tienen la misma suma que los n
siguientes (en números de 2n cifras)
Primo equilibrado
Primo equilibrado es aquel que es promedio de su primo anterior y el siguiente.
Dos
conjuntos se llaman equipotentes si es posible establecer entre ellos
una correspondencia biyectiva.
Los dos conjuntos tendrán
el mismo cardinal.
Números especulares
Dos números naturales se llaman especulares para la multiplicación cuando sus imágenes especulares dan el mismo producto que ellos. Por ejemplo:
23*64 = 46*32
Ver Potencia
F
Factor en un producto
Se llaman factores en un producto a los dos o más números que se multiplican.
Factorial de un número
Llamaremos factorial de un número natural n al producto
n! = n(n-1)(n-2)(n-3).....3.2.1
También se llama factorial de n de grado k y diferencia d al producto
a(a-d)(a-2d)..... (hasta k factores)
Si la diferencia es d=1, el factorial se representa por
a(n = a(a-1)(a-2)(a-3).....(a-k+1)
Es fácil demostrar que a(n es divisible entre n!
Número feliz
Se define el siguiente algoritmo: Dado un número entero positivo expresado en el sistema de numeración decimal, se suman los cuadrados de sus dígitos, con lo que obtenemos otro número entero positivo. Volvemos a reiterar la operación de sumar los cuadrados de sus dígitos, y continuamos hasta llegar a 1 o a un ciclo que no lo contiene. Los números que llegan al final igual a 1 son los llamados felices, y al resto les llamaremos infelices.
El 203 es feliz, porque 22+32=13; 12+32=10; 12+02=1
Son felices, por ejemplo, 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97 y 100
4 no es feliz, porque entra en un bucle: 4, 16, 37, 58, 89, 145, 42, 20, 4…
Conjetura de Fermat (o gran teorema)
La ecuación diofántica xn + yn = zn no tiene solución para n>2
Euler la demostró para n=3 y n=4, Dirichlet para n=7 y Legendre para n=14.
En 1995 la demostró Wiles para todo n.
Ecuación de Fermat
La ecuación y2– a*x2 = 1
Si a no es un número cuadrado admite infinitas soluciones.
Sucesión de Fibonacci
Se llama sucesión de Fibonacci a la siguiente: 1, 1, 2, 3, 5, 8, ...que cumple que cada elemento es suma de los dos anteriores, definiendo además a1 como 1 y a2 como 1
Multiplicación de Fibonacci
La representación de Zeckendorf da lugar a un producto muy curioso, que consiste, dados dos números representados como suma de elementos de Fibonacci, formar un sumatorio doble en el que cada sumando sea un número de Fibonacci cuyo índice sea la suma de los índices de cada uno de los factores.
Números figurados
Se llaman así aquellos números que representan conjuntos cuyos elementos se pueden situar en forma de figura geométrica regular. Pueden ser triangulares, cuadrados, pentagonales, oblongos, etc.
Conjunto finito
Un conjunto es finito cuando es coordinable con un conjunto {1,2,3.....n} de números naturales para un cierto n, que sería su cardinal. También se caracteriza porque no es coordinable con ninguno de sus subconjuntos propios.
Llamamos fracción continua a la expresada de esta forma:
donde a es entero y b, c…son enteros positivos llamados cocientes. Toda fracción ordinaria se puede expresar de esta forma, y todo número irracional admite aproximaciones mediante desarrollos de este tipo
Número de Friedman
Es un tipo de número narcisista. Es aquel que en un base de numeración dada puede ser generado por todas sus cifras y los operadores +, - *, / y ^ (potenciación). Se permiten paréntesis para salvaguardar la jerarquía de operaciones y la alteración del orden de las cifras. También se permite concatenar dos cifras.
Los primeros números de Friedman son: 25, 121, 125, 126, 127, 128, 153, 216, 289, 343, 347, 625, 688, 736, 1022, 1024, 1206, 1255, 1260, 1285, 1296, 1395, 1435, 1503, 1530, 1792, 1827, 2048, 2187, 2349, 2500, 2501, 2502, 2503, 2504, 2505, 2506, 2507, 2508, 2509, 2592, 2737, 2916, 3125, 3159,.., pues 25=52, 121=112, 125=5(1+2), 126=21*6,...
Diremos que un número de Friedman es "agradable" si las cifras mantienen su orden en los cálculos. Los primeros de estos números son: 127, 343, 736, 1285, 2187, 2502, 2592, 2737, 3125, 3685, 3864, 3972, 4096, 6455, 11264, 11664, 12850, 13825, 14641, 15552, 15585, 15612, 15613, 15617, 15618, 15621, 15622, 15623, 15624, 15626, 15632, 15633, 15642, 15645, 15655, 15656, 15662, 15667, 15688, 16377, 16384, 16447, 16875, 17536, 18432, 19453, 19683, 19739...
Si un número de Friedman todas las cifras del 1 al 9 recibe el nombre de pandigital. Son núeros de Friedman pandigitales 123456789 = ((86 + 2 × 7)5 − 91) / 34 y 987654321 = (8 × (97 + 6/2)5 + 1) / 34
Si se permiten factoriales y raíces, se pueden descubrir otros casos de números autogenerados por sus cifras.
G
Teoremas famosos de Gauss
a) Un número natural es suma de 3 cuadrados si y sólo si no es de la forma 4a (8b-1)
b) Todo número natural es suma de a lo más tres cuadrados.
c) Todo número natural es suma de a lo más tres triangulares.
Sucesión o progresión geométrica
Es aquella sucesión en la que cada término es igual al anterior multiplicado por un número constante llamado razón. El primer término se define aparte.
Media geométrica
Ver Media
La palabra gnomon tiene varios significados en Geometría y Trigonometría. Aquí nos interesa como número figurado. Un número es de tipo gnomon cuando se pueden dibujar sus unidades como escuadras de lados iguales.
Regla de Golomb
Se le da el nombre de Regla de Golomb a un conjunto de marcas señaladas en una regla imaginaria, tal que todas las diferencias entre marcas sean distintas.
Sucesión de Golomb
Tiene una definición muy curiosa, y es que a(n) representa el número de veces que aparece n en la sucesión, si además definimos a(1)=1 e implícitamente aceptamos que cada valor de n ocupa el mínimo número de orden posible. Sus primeros elementos son:
1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12,…
Un conjunto dotado de una operación tiene estructura de grupo cuando para esa operación constituye un semigrupo y además existe un elemento neutro y cada elemento del conjunto posee un inverso. Si además posee la propiedad conmutativa diremos que el grupo es abeliano.
H
Distancia de Hamming
Hamming definió su distancia para palabra binarias como el número total de bit en los que ambas se diferencian, comparando, como es de esperar cada uno con el que ocupa el mismo lugar en la otra palabra. Así, la distancia de Hamming entre 11001011 y 11100011 es de 2, porque son diferentes entre sí los dígitos resaltados en negrita.
Número heterómero
Sinónimo de Oblongo
Número poligonal de seis lados. Su fórmula es H(n)=n(2n-1)
I
Una operación definida en un conjunto tiene la propiedad idempotente cuando para todo elemento a del conjunto se cumple
a*a = a
Por ejemplo, son idempotentes el MCD, el MCM o el orden ≤
Números iguales
Dos números son iguales cuando representan como cardinales al mismo conjunto o a conjuntos coordinables.
Número impar
Un número se llama impar si no es divisible entre 2. Se le puede representar por la fórmula 2n+1
Método de demostración de propiedades referentes a números naturales consistente en:
Demostrar la propiedad para n=1.
Demostrar que si la propiedad es cierta para n, también lo es siempre para n+1.
Con esto quedará demostrado que es cierto para todo n natural.
Por ejemplo. Demuestra así que la suma de los n primeros números impares es igual a n2.
Conjunto de tipo infinito
Un conjunto es de tipo infinito cuando es coordinable con algún subconjunto propio. Por ejemplo, el conjunto de los números naturales 1,2,3,4... es infinito, porque es coordinable con 2,4,6,8…
Elemento inverso en un grupo
Un elemento b de un grupo es inverso de otro a y se representa por a-1, cuando la operación entre ambos da como resultado el elemento neutro:
a*b = e, o bien a*a-1 = e
Si el grupo es aditivo, el inverso se suele llamar opuesto (-a) , y en ese caso se cumple a + (-a) = 0
J
Sucesión de Jacobsthal
Es una sucesión recurrente de segundo orden, definida por
X0=0, X1=1, Xn=Xn-1+2Xn-2
Sus primeros términos son: 0, 1, 1, 3, 5, 11, 21, 43, 85, 171, 341, 683, 1365, 2731, 5461, 10923, 21845, 43691,…http://oeis.org/A001045
La jerarquía de una operación es el orden de prioridad que posee en un cálculo complejo cuando no hay paréntesis presentes. Consiste en el siguiente orden:
Potencias y raíces
Multiplicaciones y divisiones
Sumas y restas
K
En 1949 este matemático indio estudió la rutina u operación que lleva su nombre. A partir de cualquier número de cuatro cifras N no todas iguales formó dos números distintos: N' formado por las mismas cifras en orden decreciente y N'' formado mediante una ordenación creciente. A la diferencia K(N) = N' - N'' la llamaremos Función de Kaplekar de N. Así K(2543) = 5432 - 2345 = 3087. Esta función puede iterarse, y formar K(K(N)), K(K(K(N))), etc. En el ejemplo K(K(2543)) = K(3087) = 7803 -3087 = 4716. Estas definiciones se extienden a número cualquiera de cifras, aunque Kaprekar sólo estudió el caso de cuatro.
Si
se itera la función de Kaprekar puede llegarse al número
cero, a una constante o a un ciclo. Este resultado depende del
número de cifras y del valor de N. En el caso de terminar en
una constante, esto se produce porque K(N)=N. Esto ocurre con el
número 495 en el caso de tres cifras y con 6174 en el caso de
cuatro (en sistema de numeración decimal), a los que se les
llama constantes de Kaprekar para ese número de cifras.
Para
dos cifras no existen constantes, pero se producen ciclos, como 9 ,
81, 63, 27, 45, 9. Para cinco cifras no existen números
invariantes respecto a la función K, pero sí se
producen ciclos. Con seis existen dos: 549945 y 631764.
L
Ley
La palabra ley puede significar en general toda fórmula, algoritmo o regla que determina la estructura o formación de un objeto matemático.
Ley de composición interna
Dado un conjunto S, llamaremos Ley de Composición Interna a toda aplicación del conjunto S×S en S, es decir, una aplicación que hace corresponder a cualquier par de elementos del conjunto S en otro elemento del mismo conjunto.
Las operaciones de sumar y multiplicar suelen estar definidas de forma que constituyan leyes de composición interna. No así la resta y la división.
Ley formal
Se utiliza como sinónimo de propiedad de una operación.
Números de Lychrel
Se llaman números de Lychrel a aquellos para los que no se sabe si el Algoritmo 196 tiene parada o no
Sucesión de Lucas
Se llama sucesión de Lucas a la siguiente: 1, 3, 4, 7, 11, 18, ...que cumple que cada elemento es suma de los dos anteriores, definiendo además a1 como 1 y a2 como 3. Es muy parecida a la de Fibonacci, con la que comparte propiedades.
M
Ver Desigualdad
Un número entero positivo “McNugget”, es aquel que es expresable como combinación lineal, con coeficientes enteros no negativos, de los números 6, 9 y 20. Se llama así porque 6, 9 y 20 eran los contenidos de las cajas de McDonald's® Chicken McNuggetsTM.
Aritmética
La media aritmética de un conjunto de números es el cociente de dividir su suma entre el número de elementos.
Geométrica
La media aritmética de un conjunto de números es la raíz de índice el número de elementos del producto de los mismos.
Armónica
La media armónica de un conjunto es el número inverso de la media aritmética de los inversos de los elementos de ese conjunto.
Contraarmónica Ver contraarmónica
Ver Desigualdad
Sucesión de Mian-Chowla
Esta sucesión se define por recurrencia de dos formas equivalentes:
(a) a(1) = 1, a(n) es el menor número mayor que a(n-1) tal que todas las sumas a(i)+a(j) con i, j ≤n son distintas.
(b) a(1) = 1, a(n) es el menor número mayor que a(n-1) tal que todas las diferencias a(i)-a(j) con i,j≤n i>j son distintas.
Primer dato de una operación de restar. Así en a-b llamamos minuendo a a y sustraendo a b.
Algoritmo (simple curiosidad) para extraer potencias de la serie natural tachando de forma periódica. Este algoritmo lo propuso Alfred Moessner y fue demostrada su validez para cualquier valor natural por Oskar Perron en 1951 usando la inducción matemática.
Propiedad monótona
Una
operación * es monótona cuando a>b implica
que a*c>b*c para todo número c del conjunto en el
que se opera.
Así, son monótonas la adición
y la multiplicación por un número positivo.
Multiplicación como operación
Operación de hallar el producto
Multiplicación "rusa"
Es una forma de multiplicar que viene de la antigüedad y se popularizó en Rusia. Requiere velocidad de cálculo mental para duplicar reiteradamente uno de los factores mientras se divide entre dos el otro (de forma entera, sin decimales). Finalmente se suman las duplicaciones que correspondan a las mitades impares. Así:
Multiplicar 23 por 120
Dividir entre dos el 23 |
Duplicar el 120 |
Sumar los correspondientes a impares |
23 |
120 |
120 |
11 |
240 |
240 |
5 |
480 |
480 |
2 |
960 |
|
1 |
1920 |
1920 |
Suma de la tercera columna |
2760 = 23*120 |
|
Consulta el modelo de Hoja de Cálculo que desarrolla esta multiplicación |
El fundamento de este método es la representación del primer número en base binaria: 23 = 2^4+2^3+2^2+1, es decir, como 11101(2. Las cifras 1 indican qué potencia se ha de sumar.
Número múltiplo de otro
Ver División
N
Sucesión de las vacas de Narayana
Sucesión similar a la de Fibonacci, con este planteamiento:
Una vaca tiene anualmente una cría. Cada una de ellas, cuando ya es novilla a los cuatro años, también tiene una cría anual ¿Cuántas vacas habrá a los N años?
Sus primeros términos son 1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60, …
Número narcisista
Un número es narcisista en el sistema de numeración decimal cuando equivale a la suma de las potencias de sus cifras elevadas todas al mismo índice. El más pequeño que se conoce es el 153, que equivale a 13+53+33 y le sigue el 370 = 33+73+03
Un narcisista impresionante es 410 + 610 + 710 + 910 + 310 + 010 + 710 + 710 + 710 + 410 = 4679307774
Un tipo de números similar es el de Friedman.
Número natural
Son los números 1,2,3,4....(a veces se incluye el 0 para algunas cuestiones), los más sencillos que existen y los primeros en ser inventados por la Humanidad. Su definición rigurosa se construye a partir de los Axiomas de Peano. Se representan por N.
El conjunto N es semigrupo para la adición y la multiplicación.
Elemento neutro
En elemento O se llama neutro para una operación * cuando a*O=O*a=a para todo a del conjunto en el que se opera. En la suma de enteros el neutro es el 0 y en la multiplicación, el 1.
Sistema de numeración
Es un conjunto de símbolos finitos y reglas que permiten representar todos los números naturales.
Sistema de numeración decimal
Es el constituido por las cifras 0,1,2,3...9 unidas mediante un sistema de representación posicional, es decir, en el que cada cifra tiene un valor distinto según su posición.
Ver Número
Automórfico, Cardinal, Cuadrado, Figurado, Heterómero,
Impar, Narcisista, Par, Piramidal, Plástico, Poligonal, Triangular, Trimórfico
Ver Números
O
Número del tipo n(n+1), siendo n un número natural.
Es toda ley que hace corresponder a cada par de elementos de un conjunto, otro elemento único de ese conjunto. Son operaciones la adición, sustracción, multiplicación, etc.
Ver inverso
Definición de relación de orden
Una relación ≤ definida en un conjunto A se llama de orden cuando cumple las tres propiedades
Reflexiva:
Para todo elemento a de A se cumple que a ≤ a
Antisimétrica:
Si dos elementos de A, a y b, cumplen simultáneamente que a ≤
b y b≤ a, entonces a=b, es decir, son idénticos
Transitiva:
Si tres elementos a, b y c de A cumplen que a ≤ b y que b ≤ c,
entonces, a ≤ b
Si un conjunto está dotado de una relación de orden, le llamaremos ordenado. Así, los números naturales están ordenados mediante la relación "menor o igual" y otras muchas.
Orden total
Los números naturales, para la relación ≤ presentan un orden total, porque para cada par de números a y b siempre se verifica a ≤ b o bien b ≤ a (son comparables).
Orden parcial
Los números naturales, para la relación de ser múltiplo presentan un orden parcial, dado que existen pares de números no comparables, como 4 y 7 que ninguno de ellos es múltiplo del otro. Buen orden
El orden natural de los números posee buena ordenación, es decir, en cada conjunto finito de números naturales podemos elegir siempre el mínimo.
Diremos que un elemento a es cota superior de un conjunto ordenado A, cuando se verifica x ≤ a "x Î A (para todo x de A). Por ejemplo, número 2 es una cota superior de los números negativos.
Si, por el contrario, se verifica a ≤ x "x Î A diremos que a es cota inferior del conjunto A. De forma similar al ejemplo anterior, el cero es cota inferior de los positivos.
Llamaremos extremo superior o supremo a una cota superior tal que no exista ninguna otra cota superior que sea inferior a ella. Si además pertenece al conjunto, la llamaremos máximo del conjunto. Así, El número 24 es el máximo de sus propios divisores 1,2,3,4,6...24, y el número 0 es extremo superior de los negativos, pero no es su máximo.
Igualmente podemos definir extremo inferior o ínfimo, y mínimo. El extremo inferior es la mayor cota inferior del conjunto. El cero es extremo inferior de los números reales positivos. El mínimo es un extremo inferior de A que pertenece al mismo A. El 1 es el mínimo divisor de cualquier otro número natural.
Un elemento es maximal en un conjunto ordenado si no existe en el conjunto otro elemento mayor que él. En un mismo conjunto pueden existir varios elementos maximales. Por ejemplo, en el conjunto 2, 3, 5, 6, 12, 15 de divisores de 60, ordenados por la relación divisor - múltiplo, los números 12 y 15 son maximales (pero no máximos). De forma simétrica se definen los minimales. En el ejemplo anterior lo serían 2,3 y 5.
P
Sucesión de Padovan
Es la sucesión definida por recurrencia:
P(0)=1, P(1)=1, P(2)=1, P(n)=P(n-2)+P(n-3)
Sus primeros términos son: 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, …
Número palindrómico (o capicúa) es aquel que es igual a su reverso. Los números de una sola cifra se consideran palindrómicos
Número pandigital
Número pandigital es aquel que contiene en su expresión decimal las diez cifras 0123456789. Se puede extender la definición a otras bases. Es sinónimo de capicúa.
Número par
Un número se llama par si es divisible entre 2. Se le puede representar por la fórmula 2n, con n natural.
Paridad de un número natural
Es el carácter par o impar de ese número.
Axiomas de Peano
El conjunto N de números naturales se puede definir axiomáticamente mediante cinco axiomas debidos a Peano:
Los números naturales son los elementos de un conjunto N en el que existe un elemento llamado 1 y una relación llamada siguiente (sg(n)) que cumple:
El 1 pertenece a N.
A cada elemento m de N le corresponde otro sg(m) llamado siguiente de m, que es único.
El número 1 no es siguiente de otro elemento.
Si dos siguientes sg(m) = sg(p) son iguales, sus antecedentes m=p también son iguales.
Si
un subconjunto C de N cumple las condiciones:
A) 1 pertenece a
N
B) Si m pertenece a C, entonces sg(m) también
pertenece a C
entonces C=N
Ecuación de Pell
Es aquella del tipo ax2+1 = y2, con a entero positivo.
Si a es cuadrado perfecto, no existen soluciones a esta ecuación, pero si no lo es, obtendremos infinitas soluciones.
Esta ecuación no la estudió Pell (fue un error de Euler, que le dio ese nombre), pero sí Fermat y Wallis.
Es útil en muchos problemas, como el de hallar números triangulares y cuadrados a la vez.
Números de Pell
Se llaman números de Pell o números lambda a los términos e la sucesión: 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461, 80782, 195025, 470832, 1136689, ..., que se obtienen mediante la fórmula de recurrencia a1 = 0, a2=1, an=2*an-1 + an-2.
Estos números coinciden con los coeficientes de la aproximación a la raíz cuadrada de 2 mediante fraciones continuas. Dicha aproximación da lugar a una sucesión de fracciones
1 |
3 |
7 |
17 |
41 |
99 |
239 |
577 |
1393 |
1 |
2 |
5 |
12 |
29 |
70 |
169 |
408 |
985 |
en la que los denominadores coinciden con los números de Pell y a los numeradores se les conoce como números de Pell-Lucas. Sus cocientes se aproximan a la raíz de 2.
Número poligonal de cinco lados. Su fórmula es P(n)=n(3n-1)/2
Sucesión de Perrin
Es la sucesión definida por recurrencia:
P(0)=3, P(1)=0, P(2)=2, P(n)=P(n-2)+P(n-3)
Sus primeros términos son: 3, 0, 2. 3, 2, 5, 5, 7, 10, 12, 17, 22, …
Número Piramidal
Es aquel tal que las unidades del conjunto que representa se pueden situar en forma de pirámide. Son sumas de poligonales consecutivos.
Por ejemplo, los piramidales triangulares serán 1, 4, 10, 20, 35, etc. y su fórmula general (n(n+1)(n+2))/6
Es un número piramidal en el que los sumandos son poligonales centrados.
Ecuación pitagórica
Es aquella que tiene la forma a2 + b2 = c2
Sus soluciones primitivas, en las que a, b y c son primos entre sí, vienen dadas por las expresiones
a=m*n, b=(n2 – m2)/2, c=(n2 + m2)/2
En las que n y m son números impares primos entre sí, con n>m
Se da el nombre de número plástico al número 1,3247179572..., raíz de la ecuación x3 = x + 1
Aparece como límite del cociente A(n)/A(n-1) en las sucesiones de Perrin y Padovan.
Número Poligonal
Es un número figurado tal que las unidades del conjunto que representa se pueden situar ordenadamente en forma de polígono. Pueden ser triangulares, cuadrados, pentagonales, etc.
Es un poligonal en el que las sumas parciales que lo forman son a su vez poligonales con un centro.
En la figura se representa un cuadrado centrado de orden 3.
Los números poligoriales se definen de forma similar a los factoriales, pero en lugar de multiplicar números naturales consecutivos, lo hacen con los números poligonales.
Un número poligorial de orden k equivale al producto de los primeros números poligonales de orden k. Por ejemplo, 180 es poligorial de orden 3, porque es el producto de los cuatro primeros números triangulares: 180=1*3*6*10.
Potencia de un número natural con exponente natural
Llamaremos potencia de exponente k de un número natural n llamado base, y la representaremos por nk, al producto n.n.n….n de k factores iguales a n.
Operación de calcular la potencia de un número
Producto de dos números
El producto de dos números naturales a y b es otro número c obtenido como b sumas reiteradas de a. Coincide con la suma reiterada a veces del número b.
Una proporción es una igualdad de dos fracciones o razones: a/b = c/d. Los números que forman una proporción se llaman proporcionales.
Cuatro números son proporcionales cuando forman una proporción entre ellos
R
Es la operación de calcular la raíz de un número.
Raíz enésima entera
Dado un número natural a, llamaremos raíz enésima entera del mismo a otro número natural s que cumpla: sn <= a < (s+1)n
Llamaremos resto de esta operación de radicación al número r que cumple: a = sn +r
Si r es igual a 0, diremos que la raíz es exacta.
Sinónimo de fracción, cociente o comparación.
Sucesión de Recamán
Es una original sucesión que Bernardo Recamán Santos envió a N. J. A. Sloane en 1991 para su colección, y que desde entonces ha originado múltiples desarrollos.
Su definición es la siguiente (versión con a(1)=1):
a(1) = 1
a(n) = a(n-1) – n, si este valor es positivo y no figura ya en la sucesión
a(n) = a(n-1) +n, en caso contrario.
Sus primeros términos son: 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8, 25, 43, 62, 42, 63, 41, 18, 42, 17, 43, 16, 44, 15, 45, 14, 46, 79, 113, 78, 114, 77, 39, 78, 38, 79, 37, 80, 36, 81, 35, 82, 34, 83, 33, 84, 32, 85, 31, 86, 30, 87, 29, 88, 28, 89, 27, 90, 26, 91, 157,… (existe otra versión que comienza en 0, idéntica a esta en todo lo demás http://oeis.org/A005132)
Es un número cuyas unidades se pueden ordenar en forma de rectángulo de lados mayores que uno.
Sucesiones recurrentes
Una sucesión es recurrente cuando, a partir de cierto índice, todos los elementos se definen en función de los anteriores.
Recurrencia lineal de primer orden
Es aquella definida por una relación del tipo xn=a1xn-1+a2
Recurrencia lineal de segundo orden
Es aquella definida por una relación del tipo xn=a1xn-1+a2xn-2+a3
Fracción reducida
Se llama fracción reducida de una fracción continua a la resultante de eliminar de la misma su últimos cocientes. También recibe este nombre a toda fracción resultante del algoritmo de los cumulantes aplicados los restos del algoritmo de Euclides.
Una
relación
binaria en
un conjunto A es un subconjunto R del producto cartesiano AxA.
Diremos que dos elementos x e y de A están relacionados,
y escribiremos aRb cuando el par (a,b) pertenezca al
subconjunto R
Un número es repidígito si en un sistema de numeración todas sus cifras son iguales, como 22222.
Un número es repituno, repuno o repunit, si en un sistema de numeración todas sus cifras son iguales a la unidad: 111111.
Sinónimo de sustracción
Resto de una división
Ver división
Sinónimo de número simétrico de otro.
S
Números de Saint-Exupery
Reciben este nombre aquellos números que coinciden con el producto de los tres lados de una terna pitagórica. El primero, como era de esperar, es 60, que es el producto de 3, 4 y 5, elementos de la terna más sencilla que conocemos. El segundo, 480, es el producto de sus dobles, 6*8*10.
Un conjunto dotado de una operación constituye un semigrupo cuando esa operación es cerrada y asociativa en ese conjunto. El semigrupo puede ser conmutativo si la operación tiene esa propiedad y también poseer un elemento neutro.
Llamaremos semifactorial de un número natural n al producto n(n-2)(n-4)(n-6).... terminando el producto en 2 o 1, según la paridad de n y lo representaremos así: n!!
Número simétrico de otro en una base dada
Llamamos reverso o simétrico de un número natural a otro número que contiene las mismas cifras pero en orden opuesto.
Sistema de numeración
Un sistema de numeración es un conjunto finito de símbolos y unas reglas de formación que permiten representar números válidos en dicho sistema.
Se llama sólido a aquel número natural cuyas unidades se pueden disponer como un paralelepípedo rectángulo de lados mayores que uno. Equivale a decir que se puede expresar como producto de tres números naturales.
Llamaremos sordo a todo número natural que no posea raíz exacta.
Sucesión de números naturales
Es toda función definida de N (conjunto de los números naturales) en N. A los elementos orígenes de la función les llamaremos índices, y a las imágenes elementos de la sucesión.
En
la práctica es una secuencia ordenada de números
naturales del tipo 2,4,7,11,12,....representada por los símbolos
a1,
a2,
a3,
a4,
...an,
... en la que an
es
el elemento y n
el
índice.
Suma de dos números naturales
La suma de dos números naturales a y b (llamados sumandos) es otro número c (llamado suma) que es el cardinal de un conjunto formado por la unión de otros dos conjuntos disjuntos cuyos cardinales son a y b. Es decir: se eligen dos conjuntos que representen a los sumandos y que sean disjuntos. Su unión representará al número suma.
La operación de sumar, o hallara la suma se llama adición.
Cada uno de los datos de una suma
Operación de restar a un número a otro b, es decir, encontrar otro número c tal que se cumpla: a=b+c
Segundo dato de una operación de restar. Así en a-b llamamos minuendo a a y sustraendo a b.
T
Ver Teoremas de Bachet de Meziriac
Nombre
dado por los pitagóricos al número diez, considerado
como número triangular..
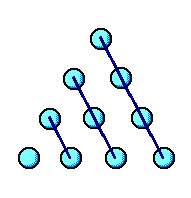
Número tetragonal
Sellaman
tetragonales a los números piramidales de tres lados.
Son
los números 1, 4, 10, 20, 35, etc. y su fórmula general
es (n(n+1)(n+2))/6
Número triangular
Un número triangular es aquel cuyas unidades se pueden situar en forma de triángulo
Los primeros números triangulares son: 1, 3, 6, 10, 15, 21, …
Todos siguen la fórmula n(n+1)/2, con n=0, 1, 2, 3, …
Sucesión de Tribonacci
Nombre coloquieal con el que se conocen los elementos de la sucesión construida como la de Fibonacci, pero usando sumas de tres en tres, es decir:
A(1)=1, A(2) = 1, A(3) = 2, y como fórmula de recurrencia A(n) = A(n-3)+A(n-2)+A(n-1) para n>3
Los primeros términos son: 1, 1, 2, 4, 7, 13, 24, ...
U
Sucesión de Ulam
Es la sucesión 1, 2, 3, 4, 6, 8, 11, 13, 16, 18, 26, 28, 36, 38, 47, ...definida por Stanislav Ulam
En ella a1=1, a2=2 y los siguientes términos son los menores números que pueden expresarse de forma única como suma de dos términos tomados entre sus anteriores. Así, 3=1+2, 4=1+3, 6=4+2. El 5 no está porque 5=2+3=1+4.
Espiral de Ulam
Es una disposición de los números en espiral en la que los números primos parecen seguir ciertas diagonales.
Números de Ulam
Se llaman números de Ulam a los que forman una sucesión construida de la siguiente forma:
Se declara u(1)=1 y u(2)=2 (esto se puede alterar) y después definiremos u(n+1) como el primer número que se pueda expresar como suma de dos números de Ulam anteriores distintos, de forma única.
Se le da el nombre de unidad al número 1, elemento neutro de la multiplicación.
W
Un número de Woodall es un número natural de la forma n · 2n − 1. Los números de Woodall más pequeños son 1, 7, 23, 63, 159, 383, 895, ...
Y
En sucesión se comienza con los valores a(1)=1, a(2)=2 y a(3)=3, y los siguientes a(n) son los números naturales más pequeños que aún no hayan aparecido en la sucesión y que tengan algún factor común con a(n-2) y ninguno con a(n-1). Para entenderlo bien podemos ir generando términos según la definición. A 1, 2 y 3 le debe seguir el 4, que es el más pequeño que comparte factores primos con el 2 pero no con el 3. Tenemos ya 1, 2, 3 y 4.
El siguiente no puede ser 5, 6, 7 ni 8. Deberá ser el 9, que comparte el factor 3 con el 3 y ninguno con el 4. Así podemos seguir generando, hasta completar:
1, 2, 3, 4, 9, 8, 15, 14, 5, 6, 25, 12, 35, 16, 7, 10, 21, 20, 27, 22, 39, 11, 13, 33, 26, 45, 28, 51, 32, 17, 18, 85, 24, 55, 34, 65,…( http://oeis.org/A098550)
Cada entero positivo puede expresarse de manera única como una suma de números distintos de Fibonacci no consecutivos. La secuencia de números de Fibonacci que se suman se denomina representación de Zeckendorf