
|
|
 |
|
|
|
|
|
|
Temas de Estadística Práctica Antonio Roldán Martínez |
|
Distribuciones bidimensionales. Correlación |
||
|
Estás en Inicio > Estadística >> Tema 4 - Distribuciones bidimensionales. Correlación. |
||
Cuestión-ejemplo
Prácticas
Ejercicios
Uso en el aula
Para ampliar
Prueba de independencia
Otros coeficientes de correlación
Resumen teórico
| Cuestión - Ejemplo |
¿Influye la primavera en estos chavales? |
La Directora de un centro está preocupada por el incremento de faltas graves que se ha producido en los primeros meses del año. Tiene a su cargo tres niveles de enseñanza A, B y C, y el seguimiento de las faltas graves lo ha resumido en la siguiente tabla:
| Meses Niveles |
Enero | Febrero | Marzo | Abril | Mayo |
| A | 4 | 6 | 7 | 8 | 8 |
| B | 3 | 3 | 6 | 5 | 9 |
| C | 9 | 7 | 7 | 13 | 14 |
¿Cómo podría estudiar bien estos datos?
¿Son independientes la distribución de faltas, el nivel de enseñanza y
los meses?
¿Qué medidas podríamos usar?
Estamos ante un caso de distribución bidimensional, porque cada falta grave se representa por dos medidas: el mes y el nivel. Siempre que las observaciones comporten dos medidas distintas para cada sujeto estaremos ante una variable bidimensional. Cada medida pertenecerá a una variable distinta, y esta puede ser nominal, cuantitativa, etc. Por ejemplo, en este caso se trata dos variables nominales, los meses y las letras A, B y C.
En esta tabla figuran frecuencias absolutas, pero veremos que también puede haber tablas con frecuencias relativas o porcentajes. Por ser una tabla de doble entrada, se le suele llamar también Tabla conjunta de frecuencias.
|
|
En el resumen teórico dispones de los distintos tipos de tablas de frecuencias que se pueden usar en estos casos. |
Tipos de frecuencia en una distribución bidimensional
Abre el documento practica41.pdf y calcula con su ayuda las frecuencias marginales y condicionadas de la tabla anterior.
Construcción de un modelo para el estudio bidimensional
A los alumnos y alumnas de un grupo de Bachillerato se les ha medido su nivel de Autoestima mediante una escala del 0 al 10, y se les ha pasado un test sobre Inteligencia Emocional que da una puntuación en una escala de 0 a 50. Los resultados los tienes en el archivo test1.ods. Lo puedes abrir ya y tenerlo preparado.
También, localiza el resumen teórico por si necesitas consultarlo.
Abre la practica42.pdf y desarrolla su contenido. Comprueba todos los resultados.
Organización de datos bidimensionales
En esta práctica aprenderás a usar tablas dinámicas. El objetivo es convertir una tabla simple de frecuencias, quizás algo desordenada, en otra más estructurada.
Abre la hoja actividad.ods. Trabajaremos sobre ella.
Abre la practica43.pdf y desarrolla su contenido.
Después de esta actividad quizás desees profundizar algo más en el tema de Tablas Dinámicas. Puedes consultar la Guía correspondiente de LibreOffice Calc
Un grupo de alumnos de Psicología han obtenido estas calificaciones en dos asignaturas:
| Psicología Evolutiva | 1 | 4 | 3 | 5 | 6 | 6 | 5 | 7 | 7 | 7 | 8 | 8 |
| Psicología Matemática II | 0 | 1 | 2 | 2 | 4 | 5 | 5 | 5 | 6 | 6 | 6 | 6 |
(1) Encuentra el valor de su Coeficiente de Pearson mediante el siguiente procedimiento:
Selecciona la tabla en este documento y pide Copiar.
Abre el archivo bidimen1.ods, selecciona la Hoja2 en cualquier celda y pide Pegado Especial como Formato HTML
Selecciona en esa Hoja2 sólo los datos numéricos.
Borra la zona de entrada de datos de la Hoja1.
Pega los datos en esa zona mediante Pegado Especial, pero acordándote de activar Trasponer, para que queden en columna.
Deberá darte R=0,9. Interpreta este resultado.
(2) Observa la Nube de Puntos que aparece junto a la tabla y coméntala. Cambia algunos datos de X o de Y hasta que consigas que el coeficiente sea menor que 0,7. ¿Qué ha ocurrido con la nube?
Calcula el coeficiente de correlación de esta distribución conjunta de frecuencias:
| Y \ X | 1 | 2 | 3 | 4 |
| 10 | 2 | 7 | 2 | 1 |
| 20 | 5 | 7 | 3 | 2 |
| 30 | 1 | 2 | 0 | 0 |
Para ello abre el modelo conjuntas.ods. que está adaptado a este tipo de tabla.
Copia estos datos en la fila de X, la columna de Y y las frecuencias en la zona amarilla. Si lo haces como en el ejercicio anterior puede que se desorganice un poco la tabla, pero si no guardas los cambios, te servirá para otra vez. Acuérdate de borrar las celdas sobrantes con Supr. También puedes borrar todo al principio con el botón correspondiente.
Debe quedar así:
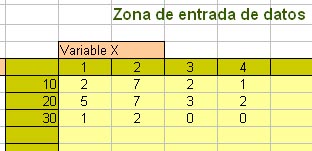
El resultado del Coeficiente de Correlación debe ser de -0,12, es decir, que estos datos no presentan correlación apreciable. Busca ese resultado en la hoja Cálculos.
Ejercicio 3
Abre el modelo ejercicio3.ods, en el que ves que figura una tabla con 20 datos bidimensionales. La variable X es nominal, de valores A,B óC, y la variable Y es cuantitativa. Mediante una tabla dinámica debes transformar esa tabla en una de doble entrada similar a la siguiente:
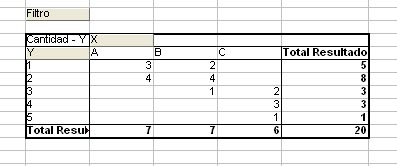
A partir de esa tabla dinámica intenta crear un gráfico lo más parecido a este:
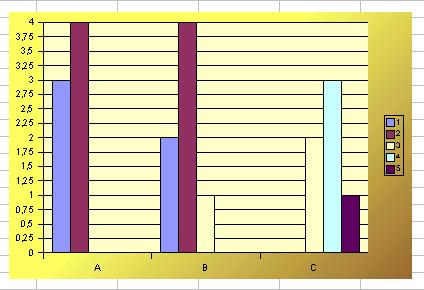
Instrumento para confeccionar tablas de frecuencias conjuntas a partir de datos dobles ingresados individualmente. De una tabla de pares se construye una tabla de doble entrada y se calculan las medias, las frecuencias marginales, los gráficos, etc.
Cuando los datos de una variable bidimensional vienen dados en una tabla de doble entrada (frecuencias conjuntas), el programa LibreOffice.org Calc no puede usar funciones como COVARIANZA, COEF,DE,CORREL, etc. En este modelo dispondrás de un esquema que te permitirá realizar los cálculos en este tipo de distribuciones de frecuencias. La segunda hoja de cálculos está protegida. No olvides dejar en blanco las celdas de datos que no uses.
Este otro modelo resuelve otra situación no prevista en LibreOffice.org Calc, y es cuando cada para de datos (X,Y) existe una frecuencia, con lo que para resolverlo con las funciones implementadas habría que repetir cada par tantas veces como indique su frecuencia, lo cual es desaconsejable si esas frecuencias son muy altas. Además, con este modelo, puedes conocer las funciones de matriz y parte de la teoría.
Mediante esta hoja podrás efectuar simulaciones de datos bidimensionales que posean promedios y variabilidad determinadas, y en los que se podrá concretar el grado de correlación y la pendiente aproximada de la nube de puntos. Es útil para estudiar la conexión entre la forma de la nube de puntos y el coeficiente de correlación.
En este documento se contiene una introducción casi experimental del significado del coeficiente de correlación. Su desarrollo es totalmente empírico y no pretende impartir teoría, sino ayudar a ver qué mide dicho coeficiente.
La Prueba de Independencia o Test de Homogeneidad investiga si existe un buen grado de asociación entre dos variables que se estudian conjuntamente, o bien son independientes. Usa la distribución chi-cuadrado, que estudiarás más adelante.
Abre el modelo homogen.ods.
Sobre él desarrolla lo explicado en el documento ampliar4.pdf
Otros coeficientes de correlación
El coeficiente de correlación de Pearson es adecuado para datos cuantitativos de intervalo o razón. En el caso de variables nominales, ordinales o dicotómicas se usan otros coeficientes, aunque algunos de ello se reducen en sus cálculos al coeficiente de Pearson.
Abre la hoja otroscoef.ods, que la usarás en el estudio del documento otroscoef4.pdf