Estás en  Inicio >    Sin decimales >   Divisibilidad > Rutas de los números primos

Consideraciones sobre la espiral de Ulam

En qué consiste la espiral de Ulam

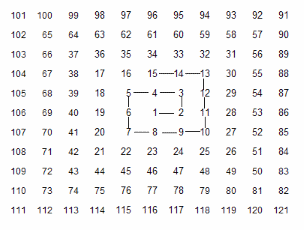
La espiral de Ulam está formada por todos los números naturales dispuestos en forma de espiral. tal como puedes ver en la imagen de abajo. Estudia la forma en la que se ordenan los números para formar la espiral de Ulam (hay otras posibilidades, que llevan a los mismos resultados con pequeñas diferencias). La espiral de la imagen comienza en el número 1, pero se puede usar cualquier otro como origen.

Anécdota

Esta disposición en espiral es debida al matemático Stanislaw M. Ulam, el cual, según se cuenta, la imaginó durante una aburrida conferencia a la que asistía en 1963. Cuando dispuso los números naturales en espiral y destacó los números primos, se llevó una gran sorpresa al comprobar que se situaban mayoritariamente en ciertas diagonales. Desde entonces esta espiral de números se hizo muy popular, porque en ella, como se ha indicado, los primos parecen seguir pautas diagonales discontinuas, aunque con tramos muy destacables llenos de primos, como puedes observar en la siguiente imagen.

Esta imagen ha sido obtenida mediante la hoja de cálculo ulam.ods, rebajando la escala de visionado de la misma.

Formas cuadráticas en la espiral

Desde la invención de esta disposición en espiral, se relacionaron las diagonales con formas cuadráticas, y en concreto, con las fórmulas clásicas de generación de números primos, como n² + n + 17, que produce primos hasta n=16, en el que falla: 19, 23, 29, 37, 47, ....A partir del 16, aunque con fallos, la fórmula sigue generando primos. Como veremos más adelante, esta forma cuadrática, a partir de un número, sitúa sus resultados en dos diagonales paralelas, que contendrán una gran densidad de primos. En la imagen los números primos están coloreados en verde y los compuestos en rojo. Se  percibe claramente que predominan los primos

Igual ocurre con otra fórmulas generadoras de primos, como n² - n + 41.

Intenta conseguir una imagen similar a la anterior, con la forma cuadrática n² - n + 41. Para ello sigue estos pasos:

• Abre la hoja de cálculo ulam.ods
• Desactiva todas las condiciones.
• Activa Ver formas cuadráticas
• Escribe los tres coeficientes 1, -1 y 41
• Activa Destacar primos

Puedes fijar en 3000 el número aproximado de elementos.

Deberás conseguir esta imagen, en la que destaca el absoluto predominio de los números primos.

Prueba ahora con una forma cuadrática que se pueda descomponer con coeficientes enteros, como n² - 17n + 30, y no obtendrás ningún primo, y con n² - 14n + 28 sólo conseguirás el número primo 11, y todos los demás compuestos.

Es claro que si una forma cuadrática admite una factorización del tipo (n-a)(n-b), con a y b naturales, a partir de los valores superiores a a y b, no podrá contener ningún primo, por lo que estos abundarán más en las diagonales engendradas por formas cuadráticas que no se puedan descomponer de esta forma.

En lo que sigue, en lugar de intentar estudiar en qué diagonales pueden estar contenidos los números primos, deduciremos en cuales no podrán darse primos desde algún valor en adelante. Para ello introduciremos los conceptos de coordenada en la espiral de Ulam y categoría rectangular de los números..

Coordenadas en la espiral

Para entender bien lo que sigue definiremos dos coordenadas para cada número natural situado en la espiral de Ulam. Es importante advertir que esta definición depende de una cierta disposición de los números en la espiral, que no es única. Nos basaremos en la disposición que usa la hoja ulam.ods.

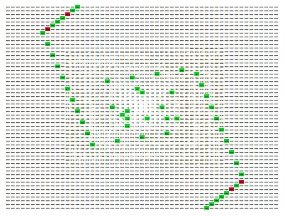
Para definir la primera coordenada consideraremos los números oblongos, que son los que se pueden representar mediante el producto n(n+1) con n natural: 2, 6, 12, 20, 30, 42, 56, 72, 90, ....Estos números dividen al conjunto de números naturales en intervalos de longitud creciente, representados en la espiral de Ulam en la imagen de abajo. Es fácil ver que cada par de números oblongos consecutivos definen un gnomon, o disposición angular. En la figura puedes observar que esos gnomones se encajan para formar rectángulos de magnitud creciente. Definiremos, para cada número, como primera coordenada de Ulam U1 al número de orden del gnomon al que pertenece. Así, los números se clasificarán según su coordenada:

U1 = 1:    1, 2
U1 = 2:    3, 4, 5, 6
U1 = 3:    7, 8, 9, 10, 11, 12
U1 = 4:    13, 14, 15, 16, 17, 18, 19, 20
...

Las amplitudes de los intervalos serán a = (n+1)n - n(n-1)  = 2n, por lo que crecerán de 2 en 2

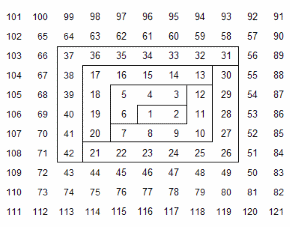
Dado un número natural k, su primera coordenada se calculará como el número U1 tal que U1(U1-1) < k <= U1(U1+1). Así, el número 130 está entre 11*10 y 11*12, luego su primera coordenada será U1=11

La segunda coordenada U2 la definiremos como k - U1(U1-1), con lo que k = U1(U1-1)+U2. En el ejemplo de 130 U1 = 11, U2 = 20 y  130 = 11*10 + 20. La amplitud de su intervalo o gnomon será de 2*11 = 22 números que comparten la misma coordenada U1. Los gnomones con ángulo dirigido hacia arriba y la izquierda tendrán una primera coordenada par, y los opuestos (hacia abajo y la derecha), coordenada impar.

Hemos definido las coordenadas por lo siguiente: Para números de un mismo gnomon, las diagonales en la espiral de Ulam se forman incrementando siempre el mismo número, que resulta ser uno de estos tres: 4*U1+4, 4*U1+6 y 4*U1+2. Además, la elección entre uno de los tres depende del ángulo de la diagonal:

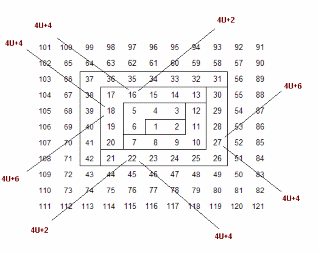
Plantéate como ejercicio comprobar que estos incrementos funcionan. Por ejemplo, en la diagonal de tipo 4U+4 formada por 4, 16, 36, 64, 100 los incrementos 12, 20, 28, 36 cumplen la expresión indicada, pues 12=4*2+4, 20=4*4+4, 28=6*4+4, 36=8*4+4,...  Se ve que esta diagonal corresponde a las coordenadas pares. Igual ocurriría con la diagonal opuesta 10, 26, 50, 82... con incrementos 16 = 3*4+4,  24 = 5*4+4, 32 = 7*4+4.

Comprueba o demuestra el resto de expresiones.

Representación rectangular de los números naturales

Todo lo que acabamos de razonar tendrá como objetivo comprobar el gran número de diagonales que "cierran el paso" a los números primos, por lo que estos han de situarse en otras diagonales.

Dado un número natural factorizado como N=a*b con a y b mayores o iguales que uno, es evidente que muchos números admiten varias factorizaciones, como 24 = 1*24 = 2*12 = 3*8 = 4*6. Llamaremos factorización de diferencia mínima a aquella en la que el valor absoluto de b-a sea mínimo. En el ejemplo sería 24 = 4*6

Llamaremos categoría rectangular C de un número N (la denotaremos por C(N) ) a la mínima diferencia (en valor absoluto) existente entre a y b al recorrer todas las factorizaciones. Por ejemplo:

C(24) = 2,porque 24 se puede expresar como 4*6, con diferencia 2

C(36) = 0, porque 36=6*6

C(19) = 18,ya que sólo se puede escribir como 19=1*19, con diferencia 18.

Esta definición es también un pequeño homenaje al protagonista de la Novela "El tío Petros y la conjetura de Goldbach", que llena los suelos de su casa de rectángulos variados, intentando componerlos para demostrar la conjetura.

Es inmediato ver que:

Los números cuadrados tienen categoría 0

Los números primos poseen categoría p-1, siendo p el número primo dado. Poseen la máxima categoría posible.

Los números del tipo n(n+1) u oblongos presentan una categoría de 1

¿Qué tiene que ver esto con la espiral de Ulam? La razón es que a partir de un número dado, todos los que poseen una misma categoría rectangular se sitúan en la misma diagonal. En realidad son dos direcciones opuestas, que comienzan a partir de un elemento dado de la categoría.

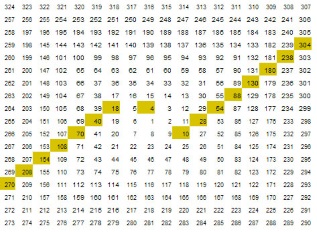
En esta imagen puedes ver las diagonales que forman los números de categoría 3 a partir del 10: 10 = 2*5, 18 = 3*6, 28 = 4*7

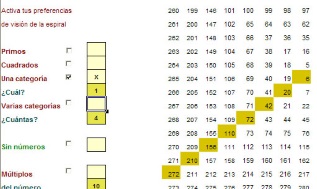
Si deseas ver las diagonales que forman los números de una categoría dada, abre ulam.ods y activa, en el panel lateral, el ver una categoría, y elige la que desees.

Aquí puedes estudiar las diagonales de los números cuadrados

En la siguiente imagen puedes ver cómo se ha elegido ver la diagonal de la categoría 1 (números oblongos):

Hemos comprobado que ciertas categorías se sitúan en una misma diagonal. ¿Será siempre así? ¿Qué relación tendrán con la distribución de los números primos? Lo veremos a continuación:

Relación entre categorías rectangulares y diagonales

Proposición: Todos los números de una categoría, a partir de uno de ellos, admiten la misma representación como una de estas dos formas cuadráticas:

Forma 1: N = (n-d)(n+d) =  n² - d²  para categorías pares

Forma 2: N = (n-d)(n+d+1) = n(n+1)- d(d+1) para categorías impares

siendo n y d números apropiados

En efecto, si un número de categoría D admite la factorización de diferencia mínima N = a*b con a<b, se podrá expresar el producto como N = a*(a+D).

Podemos usar los cambios de variable n = a+ENT(D/2), d = ENT(D/2), siendo ENT la parte entera, con lo que la factorización quedará como N = (n-d)(n+d) en el caso par y N = (n-d)(n+d+1) en el caso impar, si n es mayor que d..

Desarrollando ambas expresiones tendremos que los números de categoría par podrán representarse mediante formas cuadráticas del tipo N = n² - d²  y los de categoría impar como N = n⁽n+1)- d(d+1)

Por ejemplo 18, de categoría 3, 18 = 3*6 = (4-1)(4+2) = 4(4+1) - 1(1+1) que corresponde a la forma cuadrática n⁽n+1)- d(d+1)

13 = 1*13 = (7-6)(7+6) = 7² - 6²   que corresponde a la forma cuadrática  n² - d²   correspondiente a la categoría par.

20 = 4*5 = (4-0)(4+1) = 4(4+1) -0*(0+1)

En resumen

Los números de categoría par (incluyendo los primos salvo el 2) se pueden expresar, a partir de uno de ellos, como diferencia de dos cuadrados n² - d², en el que el sumando d² es el mismo en  toda la categoría

Los números de categoría impar desde uno en adelante equivalen a la diferencia entre dos números oblongos N = n⁽n+1)- d(d+1), de los que el segundo se mantiene constante en toda la categoría

Por ejemplo, 19 = 10² - 9²     24 = 5² - 1²     35 = 6² - 1²  28 = 6*5 - 2*1    14 = 5*4 - 3*2

Si un número de categoría par tiene como expresión N = n² - d²  , su consecutivo en la categoría será N' = (n+1)² - d²  y el siguiente N'' = (n+2)² - d² . Es interesante la diferencia entre N'' y N:

N'' - N = (n+2)² - d² - n² + d²  = 4n + 4

Si un número de categoría impar tiene como expresión N= n(n+1) - d(d+1), el que ocupa dos lugares más arriba será N'' = (n+2)(n+3) - d(d+1)  y su diferencia:

N'' - N = (n+2)(n+3) - d(d+1) - n(n+1) + d(d+1) = 5n + 6 - n = 4n + 6