|
|
|
|
|
|
|
Estás en Inicio > Sin decimales > Divisibilidad > Rutas de los números primos
Rutas en un triángulo isósceles
Hoja de cálculo Ruttriang
Descripción de la hoja
El objetivo de esta hoja es similar al que construye la espiral de Ulam: ordenar los números naturales siguiendo unas rutas, que en este caso son las hipotenusas de triángulos isósceles crecientes.
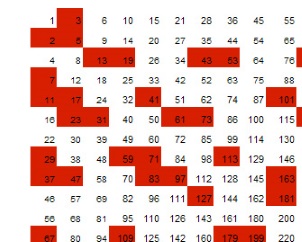
Se puede observar en la imagen la disposición en diagonal recorriendo de forma consecutiva la sucesión de números naturales.
Los controles para decidir el tamaño y tipo de este esquema triangular son muy simples:
Se decide con qué número se inicia la sucesión natural (por defecto el 1. Si no se indica lo contrario, se supone que es el número inicial) y el lado del triángulo, es decir, el número tanto de filas como de columnas. Para números altos se puede ralentizar el proceso.
Se puede desear destacar un tipo de números. Se observa en la versión actual que podemos destacar los primos, cuadrados, múltiplos de un número o triangulares (este último con una pequeña y natural sorpresa)
Una vez concretados los parámetros, con el botón Iniciar se construye el triángulo.
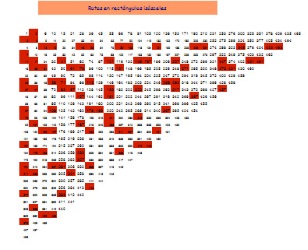
En la imagen se ha construido un triángulo isósceles de lado 30 con los números primos destacados.
En él se aprecian varios hechos:
La primera fila está compuesta por los números triangulares, ninguno de los cuales, salvo el 3, es primo ¿Por qué?
Sobre este esquema plantearemos la siguiente cuestión:
![]() Existen filas en las
que no figura ningún número primo, y estas son las de orden 7, 11, 16, 22, ...y
en otras, como la 1, la 2 y la 4, sólo alguno al principio. ¿Cuál es la
causa?
Existen filas en las
que no figura ningún número primo, y estas son las de orden 7, 11, 16, 22, ...y
en otras, como la 1, la 2 y la 4, sólo alguno al principio. ¿Cuál es la
causa?

La demostración no es fácil, por lo que se indican a continuación los posibles pasos para lograrla. Quizás alguien pueda simplificarlos.
a) Si llamamos x al número de fila en la que figura un número M e y su número de columna, este número M viene dado por la expresión (u otra similar)
(1) M = Y2/2 +(2x-1)/2 +(x-1)(x-2)/2
Es una expresión de segundo grado tanto en x como en y, debido a que las filas y columnas son sucesiones aritméticas de segundo grado.
Si, por ejemplo x=7, entonces M = (y^2+13y +30)/2 que se descompone en (y+3)(y+10)/2, y como uno de ellos es siempre par, el resultado es un número compuesto (¿con toda seguridad?). Por tanto, no existen números primos en esa fila.
Comprueba también para 11, 16 y 22.
b) Podríamos plantearnos la solución general obligando al discriminante de la expresión (1) a ser igual a un número natural al cuadrado.
(2x-1)2 - 4(x-1)(x-2) = n2
desarrollando se llega a la expresión
8x - 7 = n2 ; x = (n2 + 7 )/8
el número x ha de cumplir esta condición para que no existan primos en su fila.
Es claro que si n es par, la condición no se cumple, y que si es impar se cumple con toda seguridad (intenta demostrarlo)
Para los valores de n 1,3,5,7,9... se tendrán las filas 1, 2, 4, 7, 11, 16, 22,...
c) Ya tenemos los números de filas que no contendrán números primos ¿Por qué no se cumple para 1, 2 y 4?
En esas tres filas se cumple la propiedad salvo en los primeros números.
Investiga la causa.
Recuerda que n ha de ser impar, es decir, de la forma 2k+1, y que M es entero y positivo, y que la descomposición en factores del número M, según todo lo anterior, es:
M = (Y + x + k -1)(Y + x + k)/2
Ahora sólo tienes que estudiar cuándo uno de los factores es igual a 1 y el otro un número primo Ya es fácil.
Se deja como partida de futuras búsquedas la siguiente imagen global, que sugiere diagonales y verticales de números primos
