
|
|
 |
|
|
|
|
Estás en Inicio > Sin decimales > Congruencias > Estrellas y congruencias

Este material no será objeto de actualizaciones.
Estrellas y congruencias
Antonio Roldán Martínez 2005
Polígonos estrellados
Las operaciones con restos tienen mucho que ver con otras cuestiones, por
ejemplo con los polígonos estrellados.
Sigue las instrucciones
para verlo.
Abre la hoja de cálculo que estudia los polígonos estrellados
|
|
estrellados.xls
|
|
|
estrellados.ods
|
Comienza por familiarizarte con él
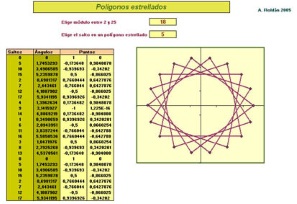
Sólo debes concretar el número de lados (módulo) que tendrá tu polígono y el salto que habrá entre un vértice y otro (salto).
¿Qué módulo y salto tendría el siguiente polígono? Ve probando hasta acertar.
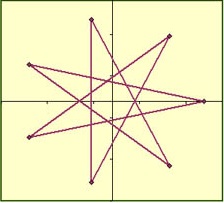
Experimentamos con polígonos estrellados
Concreta el módulo en 9 y el salto en 1.Observa que obtienes un eneágono
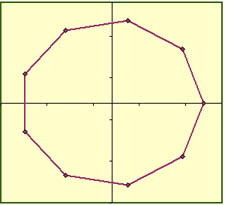
Escribe como salto el 6 ¿Qué obtienes? Escríbelo aquí: _______________________
Observa la columna de saltos: ser repiten los números 0,6,3,0,6,3...
Como cada vez que sumas 6, los resultados sólo pueden ser 6,3 y 0, se ha formado un triángulo.
Prueba ahora con todos los números del 1 al 8:
Rellena esta tabla con los números por donde pasa el polígono
que se dibuja y escribe un comentario breve detrás.
Ya tienes rellena
la fila del 6.
| Núm. |
Saltos |
Comentarios | |||||||
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | 6 | 3 | 0 | 6 | 3 | 0 | 6 | 3 | Se forma un triángulo normal |
| 7 | |||||||||
| 8 | |||||||||
¿Qué números consiguen que se cierre un polígono normal (que no tenga forma de estrella)? ________________________________
¿Con cuáles de ellos se consigue pasar por todos los vértices posibles? ______________________________
Por último, ¿qué números forman un polígono estrellado? _______________________________________
Todos los números del 1 al 8 deberás incluirlos en alguna clase.
Hay parejas de números que forman la misma figura, aunque sea un poco
girada. ¿Sabrías escribir todas las parejas?
Por ejemplo, el 4
y el 5 forman el mismo polígono estrellado. Escribe las demás:
______________________________
Generadores de los polígonos estrellados
Observa bien:
Los números 3 y 6 forman un _____________, el 1 y 8 forman un ________________________ y los demás, 2, 4,5 y 7 forman un _______________________
Ahora debes intentar ver por qué unos números forman unas figuras y otros forman otras.
Antes de responder, si no lo tienes claro, quizás te convenga ver otro
ejemplo.
Elige módulo 10 y repite el trabajo
| Núm. | Saltos | Comentarios | |||||||
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | |||||||||
| 8 | |||||||||
| 9 | |||||||||
Ahora hay números que forman un pentágono normal, que son _________
Otros forman un pentágono estrellado, el ____ y el _____
Otros dos forman un decágono normal, que son ____________
¿Se forma algún decágono estrellado?
Ahora deberías decidirte:
Para cualquier módulo, ¿Qué números
no consiguen pasar por todos los vértices, sino que cierran un polígono
con menos número de lados? (Es algo relacionado con divisores)
¿Cómo son los números que dibujan un polígono
(estrellado o no) que pase por todos los vértices?
De esos, ¿cuáles no producen estrellados?
Resume:
Con módulo 9 se producen _______ polígonos estrellados distintos, usando saltos de ___________ vértices
Con módulo 10 se producen _______ polígonos estrellados distintos, usando saltos de ___________ vértices
Prueba ahora, experimentando antes, a rellenar estas afirmaciones:
Con módulo 6 se producen _______ polígonos estrellados distintos, usando saltos de ___________ vértices
Con módulo 7 se producen _______ polígonos estrellados distintos, usando saltos de ___________ vértices
Indicador de Euler
A cada número natural n le podemos asignar un número, llamado indicador de Euler y representado por f(n) y se halla contando todos los números más pequeños que n y que no tienen divisores comunes con él (es decir, son primos con él)
¿Tendrá algo que ver ese indicador con los polígonos estrellados?. Reflexiona siguiendo estos pasos:
El indicador de 9 es 6, porque los números 1, 2, 4, 5, 7 y 8 no son
divisibles por 3, que es el único divisor primo de 9.
Por otra parte has visto que con módulo 9 se producen 2 polígonos
estrellados diferentes (en realidad cuatro (los formados por 2, 4, 5 y 7, pero
son iguales dos a dos)
El indicador de 7 también es 6 (¿por qué?) y también tiene 2 polígonos estrellados diferentes.
¿Qué relación habrá?
Intenta descubrirla rellenando antes este tabla
| Número n | Indicador f(n) | Número de polígonos estrellados |
| 5 | ||
| 6 | ||
| 7 | 6 | 2 |
| 8 | ||
| 9 | 6 | 2 |
| 10 | ||
| 11 | ||
| 12 |
Ahora la pregunta definitiva
¿Sabrías encontrar una fórmula que aplicada al indicador f(n) nos diera el número de polígonos estrellados de n vértices?
Reflexiona y pide ayuda si la necesitas