
|
|
 |
|
|
|
|
 |
Temas de Estadística
Práctica Antonio Roldán Martínez |
|
|
Contraste de hipótesis |
||
|
Estás en Inicio > Estadística >> Tema 8 - Contrastes de hipótesis |
||
| Cuestión - Ejemplo |
Creo que vamos a peor... |
Un director de un colegio tiene una especial preocupación por el alumnado de difícil comportamiento. Ha elaborado un criterio objetivo para calificar a ciertos alumnos o alumnas como conflictivos. Se basa en las faltas de asistencia, retrasos, calificaciones trimestrales partes de disciplina, etc. Lleva años calificando como conflictiva a una parte del alumnado, que supone, por término medio el 12% de la población estudiantil de la que procede su alumnado.
Últimamente está observando un incremento del porcentaje de este tipo de calificaciones. En efecto, en el presente curso, con una matrícula de 1385, el colegio presenta un número medio de 201 calificaciones de conflictividad. ¿Puede seguir manteniendo la hipótesis de que sólo supone un 12% del total?
Esta cuestión es un ejemplo claro de un contraste de hipótesis estadística. El director hace una afirmación o tiene una creencia: el grado de conflictividad es del 12% del alumnado. Los hechos, sin embargo, parecen hacerle sospechar que esto ya no es cierto. En efecto, el grado actual es del 201/1385 = 14,5%
En estos casos surge siempre una duda: La diferencia que observo, ¿es debida al azar o a que en realidad la población estudiantil ha cambiado?
Teóricamente, es imposible responder con seguridad a esta pregunta por lo que lo haremos en términos de probabilidad: Los 1385 alumnos y alumnas de este año constituyen una muestra de la población total. Si presentan un 14,5% de conflictividad puede ser debido a que en la actual promoción ha llegado al colegio, por puro azar, un alumnado de peor comportamiento que la media. Pero también puede ocurrir que haya cambiado toda la población.
Si calculáramos la probabilidad de que ocurra lo primero (por puro azar) y nos resultara muy pequeña, nos inclinaríamos más bien al caso contrario (que ha cambiado la población). Si la probabilidad fuera razonable, por prudencia, mantendríamos la hipótesis del 12%.
¿Qué es una probabilidad pequeña o una probabilidad razonable? Según el tipo de trabajo estadístico que se emprenda, se suele tomar como límite 0,1, 0,05 ò 0,01.
 |
En el resumen teórico puedes repasar los conceptos de los Contrastes (o tests) de hipótesis |
Si deseamos efectuar un contraste de hipótesis sobre la proporción, según la teoría, si np>5 se puede usar la distribución binomial, que desemboca en normal para muestras grandes.
En este caso np coincide con las 201 calificaciones de conflictividad, luego se cumple con creces. Además, conocemos P=0,12, Q=0,88 y n=1385, luego podemos pasar directamente al contraste.
En todo contraste de hipótesis se aconsejan un mínimo de pasos para concretar bien el problema:
(1) Planteamiento de las hipótesis nula y alternativa
En este caso la hipótesis previa es que el porcentaje era del 12%: H0 : P = 0,12
La preocupación del director se justifica por la sospecha de que la proporción ha aumentado, luego: H1 : P> 0,12
Así que planteamos una hipótesis de tipo unilateral
por la derecha.
(2) Supuestos del contraste
Un contraste de proporción con una muestra tan grande se comporta como si la población fuera normal, por lo que podemos suponerla.
Suponemos muestra aleatoria simple procedente de una
población normal.
(3) Estadístico de contraste
Para la elección del contraste debes consultar los manuales de Estadística o el apartado de teoría de este tema. En este caso usaremos
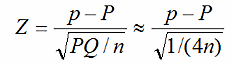
Es mucho más cómodo en nuestro caso usar la hoja de cálculo tproporcion.ods, que contiene este contraste en su primera hoja "Una proporción", y tan sólo necesitamos rellenar los datos:
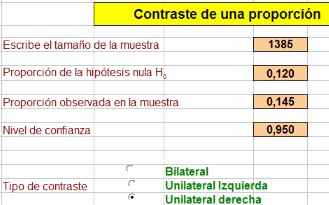
En la imagen vemos incorporado el dato del tamaño de la muestra, 1385, la proporción de la hipótesis nula, 0,12, y la alternativa de 0,145.
También se ha elegido ya el contraste unilateral por la derecha, porque el objetivo es contrastar si la proporción ha aumentado.
(4) Nivel de significación
Ya se explicó que los niveles más usados son los de 0,1, 0,05 y 0,01. Su complemento a 1 recibe el nombre de Nivel de confianza, que por tanto tendrá usualmente los valores de 0,90, 0,95 y 0,99
En el caso de Ciencias Humanas se suele elegir el 0,95. Así se ha hecho en nuestro caso.
(5) Toma de decisión
Si observas la parte inferior del esquema de contraste podrás entender cómo se toma la decisión.
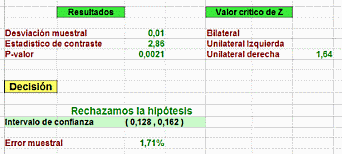
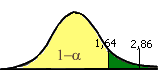
El estadístico de contraste presenta un valor de 2,86, que en la distribución normal está más a la derecha que el valor crítico de 0,95 que ves que es 1,64, luego el estadístico se sitúa en la zona de rechazo.
Otra forma de verlo es con el p-valor, que es la probabilidad, si la hipótesis nula fuera cierta, de que se produzca un resultado del 14,5%. Lee en el esquema su valor, que es de 0,0021, algo muy cercano a cero, prácticamente imposible. Por tanto, nuestra decisión debe ser:
Se rechaza la hipótesis nula
La población de estudiantes ha cambiado.
(6) Intervalo de confianza
A veces, cuando se rechaza un hipótesis, es conveniente proponer una alternativa. Podemos conseguirlo estimando el verdadero valor que tiene la proporción ahora. Esto se consigue construyendo un intervalo de confianza (generalmente bilateral) para el nuevo dato de la población.
En nuestro caso sería el de (0,128, 0,162), es decir, entre un 12,8% y un 16,2%, con un error de estimación del 1,71%. Resulta muy afinado porque la muestra es grande.
Ten preparada la hoja tmedia.ods
Desarrolla la práctica según el documento practica81.pdf
Abre la hoja tvarianza.ods
Úsala para desarrollar la práctica contenida en el documento practica82.pdf
Se sospecha que un dado está cargado, y que la cara 1 sale más veces que las
demás. Se tira el dado 600 veces y el número 1 aparece en 115 ocasiones.
¿Podemos sospechar, con un nivel de confianza del 95%, que, efectivamente, el
dado está cargado hacia el 1?
¿Qué ocurriría con un nivel del 0,90?
Solución: El tamaño de la muestra es el número de tiradas, 600. Si deseas escribir la proporción de la hipótesis nula, que es 1/6, en la primera hoja del libro tproporcion.ods, puedes hacerlo de esta forma =1/6 y así no desperdicias decimales. De la misma forma, la proporción alternativa se puede escribir como =115/600. Escribe también 0,95 (o 95%) en el nivel de confianza y elige unilateral por la derecha. Si estudias la decisión, observarás que el estadístico está en el límite de la zona crítica. Se acepta por pocas milésimas, y eso no es satisfactorio. En estos casos se suele repetir el experimento para mayor seguridad.
Cambia el 0,95 por 0,90 y en ese caso se rechaza la hipótesis. Este ejemplo te puede servir para desconfiar de esta técnica y usarla con mucha seguridad y cuidado.
El director de la cuestión-ejemplo, planteada al principio de este documento, sigue analizando las calificaciones de conflictividad. Ahora la preocupa el diferente comportamiento según el sexo. Elige al azar un grupo de 250 chicas y descubre que están calificadas como conflictivas 30. En otro grupo de 300 chicos son 40 los problemáticos. ¿Podemos afirmar, con un nivel de confianza del 95%, que ambas proporciones son iguales?
Solución: Abre la segunda hoja "Igualdad de proporciones" del libro tproporcion.ods. Escribe los tamaños de las muestras (250 y 300) y las dos proporciones (30/250 y 40/300). te resultará una proporción conjunta de 0,127. Nos decidimos por un contraste bilateral, porque el director no parece tener una opinión previa. Observa los resultados: El estadístico de contraste -0,47 está comprendido entre los dos valores críticos -1,96 y 1,96. Otra forma de analizarlo es que su p-valor, 0,6798, está muy alejado del nivel de significación 0,05. Por tanto se acepta la igualdad de proporciones entre chicos y chicas.
La siguiente tabla representa dos medidas consecutivas realizadas a los mismos sujetos en una variable cuantitativa. Una antes de un tratamiento y la otra posterior al mismo:
| Sujetos | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Medida A | 2 | 5 | 4 | 3 | 4 | 5 | 7 | 5 | 5 | 4 | 3 | 5 | 6 | 2 | 1 |
| Medida B | 2 | 6 | 5 | 4 | 6 | 8 | 6 | 7 | 6 | 4 | 4 | 7 | 9 | 5 | 2 |
¿Se puede considerar el tratamiento eficaz, es decir, producente de una diferencia significativa en las medias de ambas medidas? Se supone que lo esperado era un aumento de la media.
Solución: Crea una tabla de diferencias entre las medidas A y B y obtendrás una diferencia media de 1,33 a favor de B y una desviación típica de 1,14. Abre la hoja tmedia.ods y abre la última hoja "Dos medias relacionadas". Rellena los datos: Tamaño 15, media 1,33, desviación 1,14, valor de hipótesis 0 (como si el tratamiento no fuera eficaz). Consideramos desconocida la varianza de la población. De esta forma el p-valor es 0,0006, lo que nos hace rechazar la hipótesis de igualdad de medias, tanto al 95% como al 99%. El tratamiento ha sido eficaz.
Esta herramienta permite realizar contrastes de hipótesis sobre medias:
(a) De una sola media
(b) Igualdad de dos medias independientes.
(c) Igualdad de medias relacionadas.
Herramienta para realizar contrastes de hipótesis sobre las proporciones:
(a) De una sola proporción
(b) Igualdad de dos proporciones
(c) De la diferencia entre dos proporciones
Permite realizar contrastes de hipótesis sobre las varianzas:
(a) De una sola varianza
(b) Igualdad de dos varianzas
Contraste para la diferencia de dos proporciones
En el Ejercicio 1 se planteó como hipótesis nula la igualdad de dos proporciones, lo que nos permitía considerar la proporción conjunta. Sin embrago, en otros casos lo que interesa es contrastar la diferencia entre dos proporciones. Por ejemplo, para analizar si una campaña de sensibilización incrementa un porcentaje en una cantidad dada.
Abre el documento ampliar8.pdf, que contiene el desarrollo.
Lo puedes leer en el documento caso8.pdf